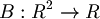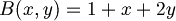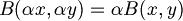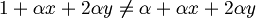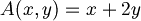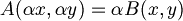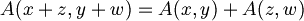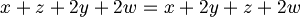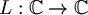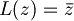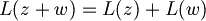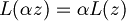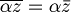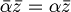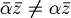Differenze tra le versioni di "Complementi di matematica"
(Soluzione esercizio 1) |
(→Soluzione esercizi) |
||
| Riga 167: | Riga 167: | ||
:Per verificare questo abbiamo principalmente due modi: | :Per verificare questo abbiamo principalmente due modi: | ||
| − | + | #I vettori vengono riscritti come prodotto delle basi, in questo caso canoniche, quindi <br><math>v_1 = 1 e_1 + 2 e_2 \qquad v_2 = 3 e_1 - 4 e_2</math><br><math>\lambda_1 (e_1 + 2 e_2) + \lambda_2 (3 e_1 - 4 e_2) = 0</math><br>Raccogliamo le due basi<br><math>e_1 (\lambda_1 + 3 \lambda_2) + e_2 (2 \lambda_1 - 4 \lambda_2) = 0 </math><br>Mettiamo le due equazioni a sistema<br><math>\begin{cases}\lambda_1 + 3 \lambda_2 = 0\\2 \lambda_1 - 3 \lambda_2 = 0\end{cases} </math><br>Risolvendolo si trova che <math>\lambda_1 = \lambda_2 = 0 </math> quindi possiamo concludere che '''sono linearmente indipendenti'''. | |
| − | + | #Un metodo molto più veloce è fare la matrice dei due vettori:<br><math>A = \begin{bmatrix}1 & 3 \\2 & -4\end{bmatrix}</math><br>che corrisponde alla matrice dei coefficienti del sistema appena sopra<br>Se verifichiamo che il determinante di questa matrice è diverso da zero allora possiamo dire che la soluzione del sistema è la soluzione banale (questa proprietà del determinante vale solo per le matrici quadrate), ovvero tutti i lambda a zero.<br><math>det(A) = - 4 -6 = - 10 \ne 0</math> <br>Anche in questo modo possiamo concludere che i vettori '''sono linearmente indipendenti'''. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
1.1b) Lo stesso per i vettori <math>v_1 = (1, 2) \quad v_2 = (3, 1) \quad v_3 = (2, -1)</math> | 1.1b) Lo stesso per i vettori <math>v_1 = (1, 2) \quad v_2 = (3, 1) \quad v_3 = (2, -1)</math> | ||
:<math>\begin{bmatrix}1 & 3 & 2 \\2 & 1 & -1\end{bmatrix}</math> | :<math>\begin{bmatrix}1 & 3 & 2 \\2 & 1 & -1\end{bmatrix}</math> | ||
:Poichè formano una matrice 2 x 3, possiamo già dire che non sono indipendenti perchè il rango massimo è 2, e il rango è il massimo numero di vettori linearmente indipendenti. | :Poichè formano una matrice 2 x 3, possiamo già dire che non sono indipendenti perchè il rango massimo è 2, e il rango è il massimo numero di vettori linearmente indipendenti. | ||
:Risposta: no, '''non sono linearmente indipendenti'''. | :Risposta: no, '''non sono linearmente indipendenti'''. | ||
| + | |||
| + | 1.2) '''Non sono linearmente indipendenti''' poichè il determinante è 0. | ||
| + | |||
| + | 1.3) '''Sono linearmente indipendenti''' poichè il determinante è diverso da 0. | ||
| + | |||
| + | 1.4) ''Boh'' | ||
| + | |||
| + | 1.5) Essendo in un campo di 3 dimensioni, basta che i tre vettori siano linearmente indipendenti infatti, il numero di dimensioni ci dice il massimo numero di vettori linearmente indipendenti tra di loro. '''E' quindi una base'''. | ||
| + | |||
| + | 1.7) Un sottoinsieme di uno spazio vettoriale è tale se è a sua volta un sottospazio, ovvero le operazioni di somma è prodotto per scalare sono chiuse (il loro risultato appartiene al sottospazio). | ||
| + | *Somma: <math>(a, a, a) + (b, b, b) = (a + b, a + b, a + b) \in V_1</math><br>Prodotto:<math>\lambda (a, a, a) = (\lambda a, \lambda a, \lambda a) \in V_1</math> <br><math>V_1</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_2</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_3</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_4</math> '''non è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_5</math> '''non è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
==Spazi euclidei e calcolo vettoriale== | ==Spazi euclidei e calcolo vettoriale== | ||
Versione delle 15:15, 11 ott 2012
Edizione 2012-2013
Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.
Indice
Richiami di algebra lineare
Prima lezione - 2 ottobre
Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi:
 : operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori
: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori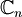 come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n
come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n![P_{n}[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) : polinomi di grado minore od uguale a n nella variabile x
: polinomi di grado minore od uguale a n nella variabile x- matrici n x m
- funzioni da
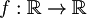 come esempio di spazio di dimensione infinita
come esempio di spazio di dimensione infinita
Sottospazi vettoriali:
- definizione di sottospazio e chiusura ripsetto alle operazioni vettoriali
- esempi concreti di verifica con calcolo della dimensione e deteminazione di una base
La lezione si è occupata prevalentemente del paragrafo 2.2 delle dispense di P. Favro ed A. Zucco che si trovano sul sito del corso.
In particolar modo è importante sapere verificare se
- dati un insieme di vettori essi siano o meno indipendenti;
- dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale;
Seconda lezione - 3 ottobre
Somma di sottospazi Y,Z di X
- l'unione Y∪Z non e' in generale un sottospazio di X
- Y+Z come minimo sottospazio contenente Y∪Z
- consistenza di Y∩Z ed unicita' della decomposizione
- somma diretta di sottospazi
Per questa parte si può fare sempre riferimento al paragrafo 2.2, in particolare a quanto scritto nelle pagine 15-16.
Enti lineari in 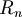
- definizione parametrica di retta
- equazione cartesiana di una retta nel piano
- equazione cartesiana di un piano in
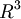
- equazione cartesiana di una retta in
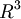 : non unicita'.
: non unicita'.
Fare riferimento a quanto scritto nei paragrafi 3.1 e 3.2. Per quanto riguarda l'equazione del piano in 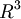 [1].
[1].
Terza lezione - 4 ottobre
Enti lineari in 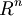 :
:
- definizione parametrica di piano k-dimensionale
- iperpiano = piano di codimensione 1
- esempio di iperpiano in
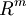 e determinazione della sua equzione cartesiana
e determinazione della sua equzione cartesiana
Operatori lineari:
- definizione ed esempi concreti di verifica
- esempio: sia
- Vogliamo sapere se la funzione B è una mappa lineare o meno; dobbiamo quindi vedere se rispetta l'additività e l'omogeneità.
- Testiamo la seconda nel seguente modo:
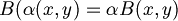 dove
dove 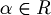
- Poichè non vale l'uguaglianza possiamo concludere che B non è una mappa lineare.
- Vediamo invece un caso in cui lo è:
- Testiamo l'omogeneità
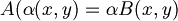 dove
dove 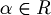
- L'uguaglianza è vera; testiamo ora l'additività:
- Poichè l'uguaglianza è vera, possiamo dice che A è una mappa lineare dallo spazio vettoriale
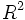 allo spazio vettoriale
allo spazio vettoriale 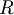
- coniugio nel campo complesso C: R-lineare ma non C-lineare
- L'additività vale in ogni caso:
- Mentre l'omogeneità vale solo se
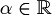
- Infatti se
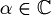 avremmo:
avremmo:
- matrice associata al coniugio, rispetto alla base reale {1, i}
- matrice associata al coniugio, rispetto alla base reale {1, 1+i}
Matrici associate ad un operatore lineare A : X → Y
Gli argomenti trattati da qui in poi sono spiegati chiaramente al paragrafo 2.8 per libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Quarta lezione - 5 ottobre
Operatori astratti A:X→Y
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Operatori lineari 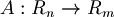
- base canonica E
- proprieta' notevole della base canonica
![[x]_{E}=x](/images/math/7/f/0/7f0b02758335d84c2f675d0617615993.png)
- azione dell'operatore nelle basi canoniche:
![Ax=[Ax]_{E}=[A]_{{EE}}[x]_{E}=[A]_{{EE}}x](/images/math/8/e/e/8eed802d2144a10f507acc87054b18df.png)
- identificazione operatore-matrice nelle basi canoniche:
![A=[A]_{{EE}}](/images/math/b/0/8/b08e44fb3e06e97ad70f9250cfa40fbb.png)
- esempi di calcolo della matrice rappresentativa in basi non canoniche
Tutti i punti sopra citati sono trattati nel paragrafo 2.8 del libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso.
- immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa
- sia
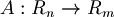 una qualsiasi mappa lineare, l'immagine di A è:
una qualsiasi mappa lineare, l'immagine di A è: 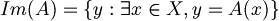
- La dimensione di
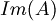 è data dal rango della matrice rappresentativa di A:
è data dal rango della matrice rappresentativa di A: ![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) , dove V è base di
, dove V è base di 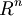 e W è base di
e W è base di 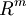
- nucleo di un operatore e sua dimensione: numero colonne - rango di ogni matrice rappresentativa
- Il nucleo di un operatore (anche detto kernel) è:
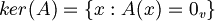 , dove con
, dove con 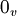 intendo il vettore nullo del codominio.
intendo il vettore nullo del codominio.
- caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa
- Sia V uno spazio vettoriale e A un'applicazione lineare, allora dim(ker(A)) + dim((Im(A)) = dim(V);
- La funzione A è iniettiva se dim(Ker(A)) = 0, ovvero se
 ;
; - La funzione A è suriettiva se dim(Im(A)) = dim(W). Ricordo che V è una base del dominio e W del codominio.
- il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'.
Soluzione esercizi
1.1a) Dire se 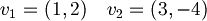 sono linearmente indipendenti.
sono linearmente indipendenti.
- In generale, diciamo che n vettori
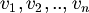 sono linearmente indipendenti quando
sono linearmente indipendenti quando
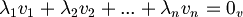 solo quando
solo quando
- (
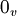 è il vettore nullo,
è il vettore nullo, 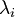 sono i coefficienti)
sono i coefficienti)
- Per verificare questo abbiamo principalmente due modi:
- I vettori vengono riscritti come prodotto delle basi, in questo caso canoniche, quindi

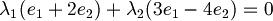
Raccogliamo le due basi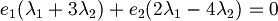
Mettiamo le due equazioni a sistema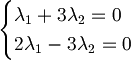
Risolvendolo si trova che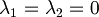 quindi possiamo concludere che sono linearmente indipendenti.
quindi possiamo concludere che sono linearmente indipendenti. - Un metodo molto più veloce è fare la matrice dei due vettori:
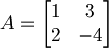
che corrisponde alla matrice dei coefficienti del sistema appena sopra
Se verifichiamo che il determinante di questa matrice è diverso da zero allora possiamo dire che la soluzione del sistema è la soluzione banale (questa proprietà del determinante vale solo per le matrici quadrate), ovvero tutti i lambda a zero.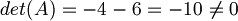
Anche in questo modo possiamo concludere che i vettori sono linearmente indipendenti.
1.1b) Lo stesso per i vettori 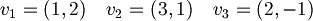
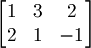
- Poichè formano una matrice 2 x 3, possiamo già dire che non sono indipendenti perchè il rango massimo è 2, e il rango è il massimo numero di vettori linearmente indipendenti.
- Risposta: no, non sono linearmente indipendenti.
1.2) Non sono linearmente indipendenti poichè il determinante è 0.
1.3) Sono linearmente indipendenti poichè il determinante è diverso da 0.
1.4) Boh
1.5) Essendo in un campo di 3 dimensioni, basta che i tre vettori siano linearmente indipendenti infatti, il numero di dimensioni ci dice il massimo numero di vettori linearmente indipendenti tra di loro. E' quindi una base.
1.7) Un sottoinsieme di uno spazio vettoriale è tale se è a sua volta un sottospazio, ovvero le operazioni di somma è prodotto per scalare sono chiuse (il loro risultato appartiene al sottospazio).
- Somma:
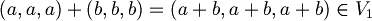
Prodotto: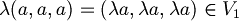
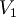 è un sottospazio di
è un sottospazio di 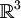
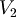 è un sottospazio di
è un sottospazio di 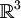
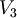 è un sottospazio di
è un sottospazio di 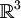
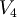 non è un sottospazio di
non è un sottospazio di 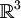
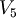 non è un sottospazio di
non è un sottospazio di 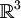
Spazi euclidei e calcolo vettoriale
Quinta lezione - 9 ottobre
Norma in spazi vettoriali reali Norma Euclidea ||x||2 in Rn e sua giustificazione tramite teorema di Pitagora Proprieta' della norma Euclidea:
- positivita' ed annullamento
- positiva omogeneita'
- disuguaglianza triangolare (senza dimostrazione, per il momento)
Assiomatizzazione del concetto di norma Esempi di norme differenti in R2
- norma del tassista ||(x,y)||1=|x|+|y|
- norma infinito ||(x,y)||∞=|x|+|y|
- geometria delle relative palle unitarie
Esempi di norme in altri spazi:
- norma Euclidea negli spazi di matrici
- norma del sup nelgi spazio di funzioni limitate
Prodotto scalare in uno spazio reale Nozione di ortogonalita' tra vettori di Rn nella norma Euclidea:
- caratterizzazione ortogonalita' tramite teorema di Pitagora
- espressione in componenti dell'ortogonalita'
- definzione di prodotto scalare Euclideo
- ricostruzione norma Euclidea a partire dal prodotto scalare Euclideo
Proprieta' del prodotto scalare < , > e sua assiomatizzazione:
- simmetria: <x,y>=<y,x> per ogni x,y
- bilinearita' che nella prima componente si scrive; <ax+bz,y>=a<x,y>+b<z,y> per ogni scalare a,b ed ogni x,z,y
- positivita' ed annullamento: x≠0 implica <x,x>>0
Norma associata ad un prodotto scalare:
- definizione ||x||2=<x,x>
- omogeneita', positivita' ed annullamento della norma
- disuguagliqanza di Schwarz e suo utlizzo per la disuguaglianza triangolare della norma
Non tutte le norme derivano da un prodototo scalare
- identita' del parallelogrammo e sue conseguenze
- il caso della norma del tassista