Differenze tra le versioni di "Complementi di matematica"
(Seconda lezione e integrazione prima) |
(Ho sistemato l'ordine dei titoli. Ora il sommario dovrebbe avere più senso.) |
||
| Riga 2: | Riga 2: | ||
''Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.'' | ''Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.'' | ||
| − | ===Prima lezione - 2 ottobre == | + | ===Richiami di algebra lineare=== |
| + | |||
| + | ==Prima lezione - 2 ottobre== | ||
| + | |||
| − | |||
Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi: | Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi: | ||
*Rn: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori | *Rn: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori | ||
| Riga 22: | Riga 24: | ||
*dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale; | *dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale; | ||
| − | + | ==Seconda lezione - 3 ottobre== | |
Somma di sottospazi Y,Z di X | Somma di sottospazi Y,Z di X | ||
*l'unione Y∪Z non e' in generale un sottospazio di X | *l'unione Y∪Z non e' in generale un sottospazio di X | ||
Versione delle 21:09, 3 ott 2012
Indice
Edizione 2012-2013
Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.
Richiami di algebra lineare
Prima lezione - 2 ottobre
Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi:
- Rn: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori
- Cn come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n
- Pn[x]: polinomi di grado minore od uguale a n nella variabile x
- matrici n x m
- funzioni da f:R→R come esempio di spazio di dimensione infinita
Sottospazi vettoriali:
- definizione di sottospazio e chiusura ripsetto alle operazioni vettoriali
- esempi concreti di verifica con calcolo della dimensione e deteminazione di una base
La lezione si è occupata prevalentemente del paragrafo 2.2 delle dispense di P. Favro ed A. Zucco che si trovano sul sito del corso.
In particolar modo è importante sapere verificare se
- dati un insieme di vettori essi siano o meno indipendenti;
- dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale;
Seconda lezione - 3 ottobre
Somma di sottospazi Y,Z di X
- l'unione Y∪Z non e' in generale un sottospazio di X
- Y+Z come minimo sottospazio contenente Y∪Z
- consistenza di Y∩Z ed unicita' della decomposizione
- somma diretta di sottospazi
Per questa parte si può fare sempre riferimento al paragrafo 2.2, in particolare a quanto scritto nelle pagine 15-16.
Enti lineari in Rn
- definizione parametrica di retta
- equazione cartesiana di una retta nel piano
- equazione cartesiana di un piano in R3
- equazione cartesiana di una retta in R3: non unicita'.
Fare riferimento a quanto scritto nei paragrafi 3.1 e 3.2. Per quanto riguarda l'equazione del piano in 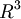 [1].
[1].