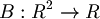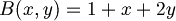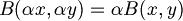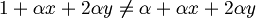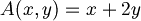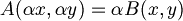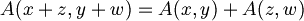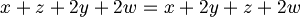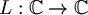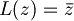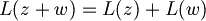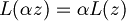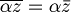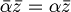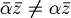Differenze tra le versioni di "Complementi di matematica"
(→Prima lezione - 2 ottobre) |
(→Quarta lezione - 5 ottobre) |
||
| Riga 137: | Riga 137: | ||
*identificazione operatore-matrice nelle basi canoniche: <math>A=[A]_{EE}</math> | *identificazione operatore-matrice nelle basi canoniche: <math>A=[A]_{EE}</math> | ||
*esempi di calcolo della matrice rappresentativa in basi non canoniche | *esempi di calcolo della matrice rappresentativa in basi non canoniche | ||
| + | |||
| + | ''Tutti i punti sopra citati sono trattati nel paragrafo 2.8 del libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso.'' | ||
| + | |||
*immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa | *immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa | ||
| − | *nucleo di un operatore e sua dimensione: numero colonne - rango di ogni | + | :sia <math>A : R_n \rightarrow R_m</math> una qualsiasi mappa lineare, l'immagine di A è: |
| + | :<math>Im(A) = \{y : \exists x \in X, y = A(x)\}</math> | ||
| + | :La dimensione di <math>Im(A)</math> è data dal rango della matrice rappresentativa di A: | ||
| + | :<math>[A]_{WV}</math>, dove V è base di <math>R^n</math> e W è base di <math>R^m</math> | ||
| + | *nucleo di un operatore e sua dimensione: numero colonne - rango di ogni matrice rappresentativa | ||
| + | :Il nucleo di un operatore (anche detto kernel) è: | ||
| + | :<math>ker(A) = \{x : A(x) = 0_v\}</math>, dove con <math>0_v</math> intendo il vettore nullo del codominio. | ||
*caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa | *caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa | ||
| + | :Sia V uno spazio vettoriale e A un'applicazione lineare, allora dim(ker(A)) + dim((Im(A)) = dim(V); | ||
| + | :La funzione A è iniettiva se dim(Ker(A)) = 0, ovvero se <math>ker(A)=\{0_v\}</math>; | ||
| + | :La funzione A è suriettiva se dim(Im(A)) = dim(W). Ricordo che V è una base del dominio e W del codominio. | ||
*il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'. | *il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'. | ||
Versione delle 17:50, 9 ott 2012
Indice
Edizione 2012-2013
Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.
Richiami di algebra lineare
Prima lezione - 2 ottobre
Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi:
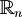 : operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori
: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori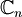 come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n
come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n![P_{n}[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) : polinomi di grado minore od uguale a n nella variabile x
: polinomi di grado minore od uguale a n nella variabile x- matrici n x m
- funzioni da
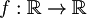 come esempio di spazio di dimensione infinita
come esempio di spazio di dimensione infinita
Sottospazi vettoriali:
- definizione di sottospazio e chiusura ripsetto alle operazioni vettoriali
- esempi concreti di verifica con calcolo della dimensione e deteminazione di una base
La lezione si è occupata prevalentemente del paragrafo 2.2 delle dispense di P. Favro ed A. Zucco che si trovano sul sito del corso.
In particolar modo è importante sapere verificare se
- dati un insieme di vettori essi siano o meno indipendenti;
- dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale;
Seconda lezione - 3 ottobre
Somma di sottospazi Y,Z di X
- l'unione Y∪Z non e' in generale un sottospazio di X
- Y+Z come minimo sottospazio contenente Y∪Z
- consistenza di Y∩Z ed unicita' della decomposizione
- somma diretta di sottospazi
Per questa parte si può fare sempre riferimento al paragrafo 2.2, in particolare a quanto scritto nelle pagine 15-16.
Enti lineari in 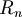
- definizione parametrica di retta
- equazione cartesiana di una retta nel piano
- equazione cartesiana di un piano in
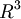
- equazione cartesiana di una retta in
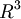 : non unicita'.
: non unicita'.
Fare riferimento a quanto scritto nei paragrafi 3.1 e 3.2. Per quanto riguarda l'equazione del piano in 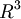 [1].
[1].
Terza lezione - 4 ottobre
Enti lineari in 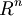 :
:
- definizione parametrica di piano k-dimensionale
- iperpiano = piano di codimensione 1
- esempio di iperpiano in
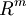 e determinazione della sua equzione cartesiana
e determinazione della sua equzione cartesiana
Operatori lineari:
- definizione ed esempi concreti di verifica
- esempio: sia
- Vogliamo sapere se la funzione B è una mappa lineare o meno; dobbiamo quindi vedere se rispetta l'additività e l'omogeneità.
- Testiamo la seconda nel seguente modo:
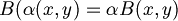 dove
dove 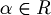
- Poichè non vale l'uguaglianza possiamo concludere che B non è una mappa lineare.
- Vediamo invece un caso in cui lo è:
- Testiamo l'omogeneità
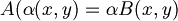 dove
dove 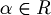
- L'uguaglianza è vera; testiamo ora l'additività:
- Poichè l'uguaglianza è vera, possiamo dice che A è una mappa lineare dallo spazio vettoriale
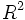 allo spazio vettoriale
allo spazio vettoriale 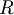
- coniugio nel campo complesso C: R-lineare ma non C-lineare
- L'additività vale in ogni caso:
- Mentre l'omogeneità vale solo se
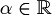
- Infatti se
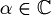 avremmo:
avremmo:
- matrice associata al coniugio, rispetto alla base reale {1, i}
- matrice associata al coniugio, rispetto alla base reale {1, 1+i}
Matrici associate ad un operatore lineare A : X → Y
Gli argomenti trattati da qui in poi sono spiegati chiaramente al paragrafo 2.8 per libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Quarta lezione - 5 ottobre
Operatori astratti A:X→Y
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Operatori lineari 
- base canonica E
- proprieta' notevole della base canonica
![[x]_{E}=x](/images/math/7/f/0/7f0b02758335d84c2f675d0617615993.png)
- azione dell'operatore nelle basi canoniche:
![Ax=[Ax]_{E}=[A]_{{EE}}[x]_{E}=[A]_{{EE}}x](/images/math/8/e/e/8eed802d2144a10f507acc87054b18df.png)
- identificazione operatore-matrice nelle basi canoniche:
![A=[A]_{{EE}}](/images/math/b/0/8/b08e44fb3e06e97ad70f9250cfa40fbb.png)
- esempi di calcolo della matrice rappresentativa in basi non canoniche
Tutti i punti sopra citati sono trattati nel paragrafo 2.8 del libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso.
- immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa
- sia
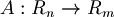 una qualsiasi mappa lineare, l'immagine di A è:
una qualsiasi mappa lineare, l'immagine di A è: 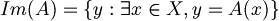
- La dimensione di
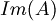 è data dal rango della matrice rappresentativa di A:
è data dal rango della matrice rappresentativa di A: ![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) , dove V è base di
, dove V è base di 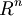 e W è base di
e W è base di 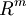
- nucleo di un operatore e sua dimensione: numero colonne - rango di ogni matrice rappresentativa
- Il nucleo di un operatore (anche detto kernel) è:
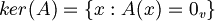 , dove con
, dove con 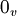 intendo il vettore nullo del codominio.
intendo il vettore nullo del codominio.
- caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa
- Sia V uno spazio vettoriale e A un'applicazione lineare, allora dim(ker(A)) + dim((Im(A)) = dim(V);
- La funzione A è iniettiva se dim(Ker(A)) = 0, ovvero se
 ;
; - La funzione A è suriettiva se dim(Im(A)) = dim(W). Ricordo che V è una base del dominio e W del codominio.
- il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'.