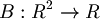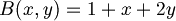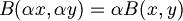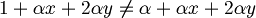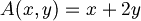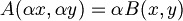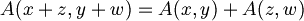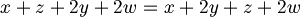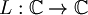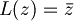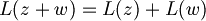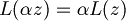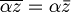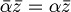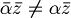Differenze tra le versioni di "Complementi di matematica"
(Consigli per lo studio - prima lezione) |
(→Settima lezione - 12 ottobre) |
||
| (43 versioni intermedie di uno stesso utente non sono mostrate) | |||
| Riga 1: | Riga 1: | ||
| − | + | Edizione 2012-2013 | |
''Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.'' | ''Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.'' | ||
| − | == | + | ==Richiami di algebra lineare== |
| − | === | + | ===Prima lezione - 2 ottobre=== |
| − | La lezione si è occupata prevalentemente del paragrafo 2.2 delle '''dispense di P. Favro ed A. Zucco''' che si trovano sul sito del corso. | + | |
| + | Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi: | ||
| + | *<math>\mathbb{R}_n</math>: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori | ||
| + | *<math>\mathbb{C}_n</math> come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n | ||
| + | *<math>P_n[x]</math>: polinomi di grado minore od uguale a n nella variabile x | ||
| + | *matrici n x m | ||
| + | *funzioni da <math>f:\mathbb{R}\rightarrow \mathbb{R}</math> come esempio di spazio di dimensione infinita | ||
| + | |||
| + | Sottospazi vettoriali: | ||
| + | *definizione di sottospazio e chiusura rispetto alle operazioni vettoriali | ||
| + | *esempi concreti di verifica con calcolo della dimensione e deteminazione di una base | ||
| + | |||
| + | ''La lezione si è occupata prevalentemente del paragrafo 2.2 delle '''dispense di P. Favro ed A. Zucco''' che si trovano sul sito del corso.'' | ||
| + | |||
| + | In particolar modo è importante sapere verificare se | ||
| + | *dati un insieme di vettori essi siano o meno indipendenti; | ||
| + | *dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale; | ||
| + | |||
| + | ===Seconda lezione - 3 ottobre=== | ||
| + | Somma di sottospazi Y,Z di X | ||
| + | *l'unione Y∪Z non e' in generale un sottospazio di X | ||
| + | *Y+Z come minimo sottospazio contenente Y∪Z | ||
| + | *consistenza di Y∩Z ed unicita' della decomposizione | ||
| + | *somma diretta di sottospazi | ||
| + | |||
| + | ''Per questa parte si può fare sempre riferimento al paragrafo 2.2, in particolare a quanto scritto nelle pagine 15-16.'' | ||
| + | |||
| + | Enti lineari in <math>R_n</math> | ||
| + | *definizione parametrica di retta | ||
| + | *equazione cartesiana di una retta nel piano | ||
| + | *equazione cartesiana di un piano in <math>R^3</math> | ||
| + | *equazione cartesiana di una retta in <math>R^3</math>: non unicita'. | ||
| + | |||
| + | ''Fare riferimento a quanto scritto nei paragrafi 3.1 e 3.2. Per quanto riguarda l'equazione del piano in <math>R^3</math>[http://it.wikipedia.org/wiki/Piano_(geometria)].'' | ||
| + | |||
| + | ===Terza lezione - 4 ottobre=== | ||
| + | |||
| + | Enti lineari in <math>R^n</math>: | ||
| + | *definizione parametrica di piano k-dimensionale | ||
| + | *iperpiano = piano di codimensione 1 | ||
| + | *esempio di iperpiano in <math>R^m</math> e determinazione della sua equzione cartesiana | ||
| + | |||
| + | Operatori lineari: | ||
| + | *definizione ed esempi concreti di verifica | ||
| + | :esempio: sia | ||
| + | |||
| + | :<math>B : R^2 \rightarrow R</math> | ||
| + | |||
| + | :<math>B(x,y) = 1 + x + 2y</math> | ||
| + | |||
| + | :Vogliamo sapere se la funzione B è una mappa lineare o meno; dobbiamo quindi vedere se rispetta l'additività e l'omogeneità. | ||
| + | :Testiamo la seconda nel seguente modo: | ||
| + | |||
| + | :<math>B(\alpha (x,y) = \alpha B(x,y)</math> dove <math>\alpha \in R</math> | ||
| + | |||
| + | :<math>B(\alpha x, \alpha y) = \alpha B(x,y)</math> | ||
| + | |||
| + | :<math>1 + \alpha x + 2 \alpha y \ne \alpha + \alpha x + 2 \alpha y</math> | ||
| + | |||
| + | :Poichè non vale l'uguaglianza possiamo concludere che B non è una mappa lineare. | ||
| + | :Vediamo invece un caso in cui lo è: | ||
| + | |||
| + | :<math>A(x,y) = x + 2y</math> | ||
| + | |||
| + | :Testiamo l'omogeneità | ||
| + | |||
| + | :<math>A(\alpha (x,y) = \alpha B(x,y)</math> dove <math>\alpha \in R</math> | ||
| + | |||
| + | :<math>A(\alpha x, \alpha y) = \alpha B(x,y)</math> | ||
| + | |||
| + | :<math>\alpha x + 2 \alpha y = \alpha x + 2 \alpha y</math> | ||
| + | |||
| + | :L'uguaglianza è vera; testiamo ora l'additività: | ||
| + | |||
| + | :<math>A(x + z, y + w) = A(x,y) + A(z,w)</math> | ||
| + | |||
| + | :<math>x + z + 2y + 2w = x + 2y + z + 2w</math> | ||
| + | |||
| + | :Poichè l'uguaglianza è vera, possiamo dice che A è una mappa lineare dallo spazio vettoriale <math>R^2</math> allo spazio vettoriale <math>R</math> | ||
| + | |||
| + | *coniugio nel campo complesso C: R-lineare ma non C-lineare | ||
| + | |||
| + | :<math>L : \mathbb{C} \rightarrow \mathbb{C}</math> | ||
| + | |||
| + | :<math>L(z) = \bar{z}</math> | ||
| + | |||
| + | :L'additività vale in ogni caso: | ||
| + | |||
| + | :<math>L(z + w) = L(z) + L(w)</math> | ||
| + | |||
| + | :<math>\overline{z+w} =\bar{z} + \bar{w}</math> | ||
| + | |||
| + | :Mentre l'omogeneità vale solo se <math>\alpha \in \mathbb{R}</math> | ||
| + | |||
| + | :<math>L(\alpha z) = \alpha L(z)</math> | ||
| + | |||
| + | :<math>\overline{\alpha z} = \alpha \bar{z}</math> | ||
| + | |||
| + | :<math>\bar{\alpha} \bar{z} = \alpha \bar{z}</math> | ||
| + | |||
| + | :Infatti se <math> \alpha \in \mathbb{C}</math> avremmo: | ||
| + | |||
| + | :<math> \bar{\alpha} \bar{z} \ne \alpha \bar{z}</math> | ||
| + | |||
| + | *matrice associata al coniugio, rispetto alla base reale {1, i} | ||
| + | *matrice associata al coniugio, rispetto alla base reale {1, 1+i} | ||
| + | |||
| + | Matrici associate ad un operatore lineare A : X → Y | ||
| + | |||
| + | ''Gli argomenti trattati da qui in poi sono spiegati chiaramente al paragrafo 2.8 per libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso'' | ||
| + | |||
| + | *<math>[x]_V</math> vettore delle componenti di x rispetto alla base V | ||
| + | *matrice <math>[A]_{WV}</math> associata ad A rispetto alle basi V in X e W in Y | ||
| + | *ricostruzione dell'azione di A a partire dalla matrice associata: <math>[Ax]_W = [A]_{WV} [x]_V</math> | ||
| + | *matrice <math>[I]_{V_1V_2}</math> associata all'indentita': matrice del cambio di base | ||
| + | *cambio delle basi ed effetto sulla matrice associata: <math>[A]_{W_2V_2} = [I]_{W_2W_1} [A]_{W_1V_1} [I]_{V_1V_2}</math> | ||
| + | |||
| + | ===Quarta lezione - 5 ottobre=== | ||
| + | |||
| + | Operatori astratti A:X→Y | ||
| + | *<math>[x]_V</math> vettore delle componenti di x rispetto alla base V | ||
| + | *matrice <math>[A]_{WV}</math> associata ad A rispetto alle basi V in X e W in Y | ||
| + | *ricostruzione dell'azione di A a partire dalla matrice associata: <math>[Ax]_W = [A]_{WV} [x]_V</math> | ||
| + | *matrice <math>[I]_{V_1V_2}</math> associata all'indentita': matrice del cambio di base | ||
| + | *cambio delle basi ed effetto sulla matrice associata: <math>[A]_{W_2V_2} = [I]_{W_2W_1} [A]_{W_1V_1} [I]_{V_1V_2}</math> | ||
| + | |||
| + | Operatori lineari <math>A : R_n \rightarrow R_m</math> | ||
| + | *base canonica E | ||
| + | *proprieta' notevole della base canonica <math>[x]_E = x</math> | ||
| + | *azione dell'operatore nelle basi canoniche: <math>Ax=[Ax]_E = [A]_{EE} [x]_E = [A]_{EE} x </math> | ||
| + | *identificazione operatore-matrice nelle basi canoniche: <math>A=[A]_{EE}</math> | ||
| + | *esempi di calcolo della matrice rappresentativa in basi non canoniche | ||
| + | |||
| + | ''Tutti i punti sopra citati sono trattati nel paragrafo 2.8 del libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso.'' | ||
| + | |||
| + | *immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa | ||
| + | :sia <math>A : R_n \rightarrow R_m</math> una qualsiasi mappa lineare, l'immagine di A è: | ||
| + | :<math>Im(A) = \{y : \exists x \in X, y = A(x)\}</math> | ||
| + | :La dimensione di <math>Im(A)</math> è data dal rango della matrice rappresentativa di A: | ||
| + | :<math>[A]_{WV}</math>, dove V è base di <math>R^n</math> e W è base di <math>R^m</math> | ||
| + | *nucleo di un operatore e sua dimensione: numero colonne - rango di ogni matrice rappresentativa | ||
| + | :Il nucleo di un operatore (anche detto kernel) è: | ||
| + | :<math>ker(A) = \{x : A(x) = 0_v\}</math>, dove con <math>0_v</math> intendo il vettore nullo del codominio. | ||
| + | *caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa | ||
| + | :Sia V uno spazio vettoriale e A un'applicazione lineare, allora dim(ker(A)) + dim((Im(A)) = dim(V); | ||
| + | :La funzione A è iniettiva se dim(Ker(A)) = 0, ovvero se <math>ker(A)=\{0_v\}</math>; | ||
| + | :La funzione A è suriettiva se dim(Im(A)) = dim(W). Ricordo che V è una base del dominio e W del codominio. | ||
| + | *il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'. | ||
| + | |||
| + | ===Soluzione esercizi=== | ||
| + | |||
| + | 1.1a) Dire se <math>v_1 = (1, 2) \quad v_2 = (3, -4)</math> sono linearmente indipendenti. | ||
| + | :In generale, diciamo che n vettori <math>v_1, v_2, .. , v_n</math> sono linearmente indipendenti quando | ||
| + | |||
| + | :<math>\lambda_1 v_1 + \lambda_2 v_2 + ... + \lambda_n v_n = 0_v </math> solo quando | ||
| + | |||
| + | :<math>\lambda_1 = \lambda_2 = ... = \lambda_n = 0 </math> | ||
| + | |||
| + | :(<math> 0_v </math> è il vettore nullo, <math>\lambda_i</math> sono i coefficienti) | ||
| + | |||
| + | :Per verificare questo abbiamo principalmente due modi: | ||
| + | |||
| + | #I vettori vengono riscritti come prodotto delle basi, in questo caso canoniche, quindi <br><math>v_1 = 1 e_1 + 2 e_2 \qquad v_2 = 3 e_1 - 4 e_2</math><br><math>\lambda_1 (e_1 + 2 e_2) + \lambda_2 (3 e_1 - 4 e_2) = 0</math><br>Raccogliamo le due basi<br><math>e_1 (\lambda_1 + 3 \lambda_2) + e_2 (2 \lambda_1 - 4 \lambda_2) = 0 </math><br>Mettiamo le due equazioni a sistema<br><math>\begin{cases}\lambda_1 + 3 \lambda_2 = 0\\2 \lambda_1 - 3 \lambda_2 = 0\end{cases} </math><br>Risolvendolo si trova che <math>\lambda_1 = \lambda_2 = 0 </math> quindi possiamo concludere che '''sono linearmente indipendenti'''. | ||
| + | #Un metodo molto più veloce è fare la matrice dei due vettori:<br><math>A = \begin{bmatrix}1 & 3 \\2 & -4\end{bmatrix}</math><br>che corrisponde alla matrice dei coefficienti del sistema appena sopra<br>Se verifichiamo che il determinante di questa matrice è diverso da zero allora possiamo dire che la soluzione del sistema è la soluzione banale (questa proprietà del determinante vale solo per le matrici quadrate), ovvero tutti i lambda a zero.<br><math>det(A) = - 4 -6 = - 10 \ne 0</math> <br>Anche in questo modo possiamo concludere che i vettori '''sono linearmente indipendenti'''. | ||
| + | 1.1b) Lo stesso per i vettori <math>v_1 = (1, 2) \quad v_2 = (3, 1) \quad v_3 = (2, -1)</math> | ||
| + | :<math>\begin{bmatrix}1 & 3 & 2 \\2 & 1 & -1\end{bmatrix}</math> | ||
| + | :Poichè formano una matrice 2 x 3, possiamo già dire che non sono indipendenti perchè il rango massimo è 2, e il rango è il massimo numero di vettori linearmente indipendenti. | ||
| + | :Risposta: no, '''non sono linearmente indipendenti'''. | ||
| + | |||
| + | 1.2) '''Non sono linearmente indipendenti''' poichè il determinante è 0. | ||
| + | |||
| + | 1.3) '''Sono linearmente indipendenti''' poichè il determinante è diverso da 0. | ||
| + | |||
| + | 1.4) ''Boh'' | ||
| + | |||
| + | 1.5) Essendo in un campo di 3 dimensioni, basta che i tre vettori siano linearmente indipendenti infatti, il numero di dimensioni ci dice il massimo numero di vettori linearmente indipendenti tra di loro. '''E' quindi una base'''. | ||
| + | |||
| + | 1.7) Un sottoinsieme di uno spazio vettoriale è tale se è a sua volta un sottospazio, ovvero le operazioni di somma è prodotto per scalare sono chiuse (il loro risultato appartiene al sottospazio). | ||
| + | *Somma: <math>(a, a, a) + (b, b, b) = (a + b, a + b, a + b) \in V_1</math><br>Prodotto:<math>\lambda (a, a, a) = (\lambda a, \lambda a, \lambda a) \in V_1</math> <br><math>V_1</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_2</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_3</math> '''è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_4</math> '''non è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | *<math>V_5</math> '''non è un sottospazio di '''<math>\mathbb{R}^3</math> | ||
| + | |||
| + | 1.15) Le rette <math>r_k, s_k</math> sono definite come l'intersezione dei piani le cui equazioni sono nei sistemi. | ||
| + | :Dobbiamo trovare il punto P in cui si incontrano, al variare di k. Per fare ciò dobbiamo trovare la soluzione al sistema unito. | ||
| + | :Uniamo i sistemi: | ||
| + | :<math>\begin{cases}x_1 + 3x_2 + x_3 = 4\\kx_1 + \qquad 2x_3 = 2\\2x_1 + kx_2 - x_3 = k -1 \\\qquad x_2 + 3x_3 = 4\end{cases}</math> | ||
| + | :Riduciamolo ad un sistema di 2 equazioni in 2 incognite: | ||
| + | :*Sommiamo la prima riga alla terza; | ||
| + | :*Moltiplichiamo la seconda per <math>\frac{3}{2}</math> e sottraiamo la quarta riga: | ||
| + | :<math>\begin{cases}3x_1 + (3 + k)x_2 = 3 + k\\\frac{3}{2}kx_1 - x_2 = -1\end{cases}</math> | ||
| + | :<math>x_2 = \frac{3}{2}kx_1 + 1</math> Sostituendo nella prima, dopo alcune semplificazioni, si arriva a | ||
| + | :<math>\frac{3}{2}x_1 (k^2 + 3k + 2) = 0</math> | ||
| + | :Se il trinomio in k si annulla (questo accade per <math>k = -1, -2</math>, l'equazione è vera per qualsiasi <math>x_1</math>: non si tratta quindi di un punto e non ha senso studiarlo. | ||
| + | :Se invece k è diverso da quei valori, l'equazione è vera solo per <math>x_1 = 0</math>. Da questo è facile trovare che <math>x_2 = x_3 = 1</math> | ||
| + | :Il punto P in cui si incontrano le rette sarà <math>P = \begin{bmatrix}0\\1\\1\end{bmatrix}</math> | ||
| + | :L'esercizio chiede inoltre di trovare l'equazione della retta <math>t</math> passante per l'origine e <math>P</math>: | ||
| + | :<math>t \rightarrow \begin{bmatrix}0\\t\\t\end{bmatrix}</math> di cui si può anche trovare l'equazione cartesiana: | ||
| + | :<math>t = \begin{cases}x = 0\\y = t\\z = t\end{cases}, t \in \mathbb{R}^3</math> | ||
| + | :e togliendo t | ||
| + | :<math>t = \begin{cases}x = 0\\y = z\end{cases}</math> | ||
| + | |||
| + | ==Spazi euclidei e calcolo vettoriale== | ||
| + | ===Quinta lezione - 9 ottobre=== | ||
| + | Norma in spazi vettoriali reali <br> | ||
| + | :La norma di <math>\|x\|</math> è la distanza del punto x dal punto 0. | ||
| + | Norma Euclidea <math>\|x\|_2</math> in <math>R^n</math> e sua giustificazione tramite teorema di Pitagora <br> | ||
| + | :Sia <math> x = \begin{bmatrix}x_1\\x_2\\.\\.\\x_n\end{bmatrix}\qquad \|x\| = \sqrt{x_1^2 + x_2^2 + .. + x_n^2}</math><br> | ||
| + | :In <math>R^2</math> è il noto teorema di pitagora: <math> x = \begin{bmatrix}x_1\\x_2\end{bmatrix}\qquad \|x\| = \sqrt{ (x_1-0)^2 + (x_2-0)^2}</math> | ||
| + | Proprieta' della norma Euclidea: | ||
| + | *positivita' ed annullamento | ||
| + | *positiva omogeneita' | ||
| + | *disuguaglianza triangolare (senza dimostrazione, per il momento) | ||
| + | Assiomatizzazione del concetto di norma: Una norma è una qualsiasi funzione che rispetta le precedenti proprietà. Per distinguere le differenti norme si pone un pedice dopo il suo simbolo. | ||
| + | La norma euclidea ha pedice 2; tuttavia, durante il corso, non si porrà tale pedice. | ||
| + | Esempi di norme differenti in <math>R^2</math> | ||
| + | *norma del tassista <math>\|(x,y)\|_2 =\|x\|+\|y\|</math> | ||
| + | *norma infinito <math>\|(x,y)\|_\infty = max(\|x\|,\|y\|)</math> | ||
| + | *geometria delle relative palle unitarie | ||
| + | Esempi di norme in altri spazi: | ||
| + | *norma Euclidea negli spazi di matrici | ||
| + | *norma del sup nello spazio di funzioni limitate | ||
| + | |||
| + | Prodotto scalare in uno spazio reale | ||
| + | :<math><x,y>= \sum_{i=1}^nx_iy_i\quad x, y \in R^n </math><br>E' quindi una funzione che associa a due vettori un elemento del campo. | ||
| + | Nozione di ortogonalita' tra vettori di <math>\mathbb{R}^n</math> nella norma Euclidea: | ||
| + | :Due vettori sono ortogonali se e solo se <math><x,y> = 0</math> | ||
| + | *caratterizzazione ortogonalita' tramite teorema di Pitagora | ||
| + | :Il teorema di Pitagora afferma che quando si tratta di triangoli rettangoli, ovvero con due lati ortogonali, si ha che | ||
| + | :<math>\|x - y\|^2 = \|x\|^2 + \|y\|^2</math>(teorema di pitagora riscritto in maniera diversa) | ||
| + | :ma poichè <math>\|x - y\|^2 = \|x\|^2 -2<x,y> + \|y\|^2</math> | ||
| + | :concludiamo che questo accade solo quando <math><x, y> = 0</math> | ||
| + | *espressione in componenti dell'ortogonalita' | ||
| + | *definzione di prodotto scalare Euclideo | ||
| + | *ricostruzione norma Euclidea a partire dal prodotto scalare Euclideo | ||
| + | Proprieta' del prodotto scalare < , > e sua assiomatizzazione: | ||
| + | *simmetria: <x,y>=<y,x> per ogni x,y | ||
| + | *bilinearita' che nella prima componente si scrive; <ax+bz,y>=a<x,y>+b<z,y> per ogni scalare a,b ed ogni x,z,y | ||
| + | *positivita' ed annullamento: x≠0 implica <x,x>>0 | ||
| + | Norma associata ad un prodotto scalare: | ||
| + | *definizione ||x||2=<x,x> | ||
| + | *omogeneita', positivita' ed annullamento della norma | ||
| + | *disuguagliqanza di Schwarz e suo utlizzo per la disuguaglianza triangolare della norma | ||
| + | Non tutte le norme derivano da un prodototo scalare | ||
| + | *identita' del parallelogrammo e sue conseguenze | ||
| + | *il caso della norma del tassista | ||
| + | |||
| + | ===Sesta lezione - 10 ottobre=== | ||
| + | |||
| + | Basi ortonormali | ||
| + | :Una base ortonormale è formata da vettori ortogonali tra loro e tutti di norma 1. | ||
| + | Relazioni tra ortogonalita' ed indipendenza: | ||
| + | *un insieme di vettori non nulli ed ortogonali a coppie e' lineramente indipendente (infatti il vettore nullo è ortogonale a qualsiasi vettore ma ne è anche dipendente) | ||
| + | *viceversa ovviamente falso | ||
| + | Definizione ed esempi di basi ortonormali, tra cui la base canonica di <math>\mathbb{R}^n</math> con prodotto scalare Euclideo <br> | ||
| + | Decomposizione di un vettore lungo una base ortonormale: | ||
| + | *calcolo delle componenti | ||
| + | *calcolo della norma | ||
| + | |||
| + | Distanza minima e proiezione ortogonale in dimensione 1 <br> | ||
| + | Problema: dato V=Rv ed x∈V determinare per la minima distanza di x da V | ||
| + | *determinare per quale t la funzione f(t)=||x-tv||2 e' minima | ||
| + | *risposta: t*=<x,v>/||v||2 | ||
| + | *x*=t*v piede della perpendicolare a V condotta da x | ||
| + | *caratterizzazione geometrica x*: <x-x*,v>=0 | ||
| + | *linearita' della mappa x→x*: rango, immagine e nucleo | ||
| + | :Data una base unidimensionale <math>v</math> e un vettore <math>x</math> di cui si vuole trovare la proiezione ortogonale<math>x_\star</math> | ||
| + | :Sappiamo intuitivamente che <math><x - x_\star, v> = 0 \quad \forall v \in V</math> però devo trovare <math>x_\star</math> | ||
| + | :Per far ciò, data la retta <math>tv</math> cerco <math>t</math> tale che la distanza da <math>x</math> sia minima, quindi | ||
| + | :<math>\psi(t)=\|x-tv\|^2</math> è la funzione che descrive il quadrato della distanza, | ||
| + | :Ne studio la derivata e vedo che è uguale a zero quando <math>t_\star = \frac{<x, v>}{\|v\|^2}</math> | ||
| + | :di conseguenza | ||
| + | :<math>f(x) = x_\star = t_\star v = \frac{<x, v>}{\|v\|^2} v</math> | ||
| + | :Dimostro che la minima distanza e la proiezione ortogonale coincidono | ||
| + | :<math><x-x_\star, v> = <x - \frac{<x, v>}{\|v\|^2} v, v> = <x,v> - \frac{<x, v>}{\|v\|^2}<v, v> = <x, v> - <x, v> = 0</math> | ||
| + | :<math>f(x)</math> è lineare poichè è lineare il prodotto scalare. | ||
| + | Enunciato e dimostrazione disuguaglianza di Schwarz, con caratterizzazione uguaglianza | ||
| + | :<math>\psi(x) = \|x-t_\star v\|^2 = \|x\|^2 - 2t_\star<v,x> + \|tv\|^2=\|x\|^2 - 2t_\star<v,x> + <t_\star v, t_\star v> = \|x\|^2 -2t_\star<v,x> + t_\star^2<v,v> = </math><br> | ||
| + | :<math>=\|x\|^2 - 2\frac{<x, v>^2}{\|v\|^2} + \frac{<x, v>^2}{\|v\|^2} = \|x\|^2 - \frac{<x, v>^2}{\|v\|^2}</math> | ||
| + | :Ciò dimostra la disuguaglianza di Schwarz infatti | ||
| + | :<math>\psi(x)\ge 0 \Rightarrow \|x\|^2 - \frac{<x, v>^2}{\|v\|^2} \ge 0 \Rightarrow \|x\|^2 \|v\|^2 \ge <x, v>^2 \Rightarrow \|x\| \|v\| \ge |<x, v>|</math> | ||
| + | :L'uguaglianza si verifica quando <math>x \in v</math> | ||
| + | |||
| + | Versione geometrica del prodotto scalare: | ||
| + | *nel Rn Euclideo, dalla trigonometria elementare <x,v>=||x||||v||cos(θ) | ||
| + | *nel caso generale, la formula precedente definisce θ | ||
| + | |||
| + | ===Settima lezione - 12 ottobre=== | ||
| + | |||
| + | Distanza minima da un sottospazio V⊂X di dimensione qualunque | ||
| + | :<math>\varphi (t_1, t_2, .. , t_k) = \|x - (t_1 v_1, t_2 v_2, ... , t_k v_k)\|^2 </math>(quadrato della distanza) | ||
| + | :Studiare il minimo di questa funzione è molto complesso quindi | ||
| + | Risoluzione geometrica, ovvero proiezione ortogonale di x∈X su V: | ||
| + | *definizione come x*∈V tale che ⟨x-x*,v⟩=0 per ogni v∈V | ||
| + | *dimostrazione unicita' di x* <br>Dimostriamo per assurdo che esista un altro <math>x_{\star\star}</math><br>Allora sarebbero vere le due equazioni<br><math><x - x_{\star\star}, v> = 0 \qquad \forall v \in V</math><br><math><x - x_{\star}, v> = 0 \qquad \forall v \in V</math><br>di conseguenza<br><math><x_\star - x_{\star\star}, v> = 0 \qquad \forall v \in V</math><br>ma poichè deve essere vero per ogni v, scegliamo <math>v = x_\star - x_{\star \star}</math><br><math><x_\star - x_{\star \star}, x_\star - x_{\star \star}> = 0</math><br><math>\|x_\star - x_{\star \star}\|^2 = 0</math> ma due punti a distanza zero coincidono! Quindi <br><math>x_\star = x_{\star \star}</math> | ||
| + | *dimostrazione costruttiva esistenza di x* tramite scelta di una base v1, ..., vk per il sottospazio V | ||
| + | *matrice di Gram associata a v1, ..., vk | ||
| + | *esempio concreto di inversione della matricie di Gram e calcolo di x* | ||
| + | Proprieta' generali della proiezione ortogonale PV su V: | ||
| + | *operatore lineare X→X | ||
| + | *immagine = V | ||
| + | *nucleo = tutti e soli i vettori di X che sono ortogonali a V | ||
| + | *PVPV=PV | ||
| + | |||
| + | Studio della matrice di Gram <br> | ||
| + | Definizione: | ||
| + | *v1, ..., vk∈X vettori assegnati | ||
| + | *matrice G=G(v1, ..., vk) definita tramite Gij=⟨vi,vj⟩ | ||
| + | *matrice quadrata simmetrica di dimensione k | ||
| + | Teorema: G invertibile se e solo se i vettori v1, ..., vk∈X sono linearmente indipendenti <br> | ||
| + | Passi chiave della dimostrazione: | ||
| + | *u=λ1v1+...+λkvk e w=μ1v1+...+μkvk generici elementi di V | ||
| + | *λ=(λ1,...,λk) e μ=(μ1,...,μk) elementi di Rk | ||
| + | *vale formula di calcolo ⟨w,u⟩=⟨μ,Gλ⟩ dove l'ultimo prodotto scalare e' quello Euclideo standard di Rk | ||
| + | *dedurne che u=0 equivale a Gλ=0 | ||
| + | *invertibilita' di G equivalente alla iniettivita' dell'operatore associato (base canonica) | ||
| + | Osservazioni: | ||
| + | *quando i vettori v1, ..., vk sono ortonormali, la matrice di Gram e' l'identita' | ||
| + | *metodo molto conveniente per valutare indipendenza lineare quando k<dim(X) | ||
Versione attuale delle 17:23, 18 ott 2012
Edizione 2012-2013
Premessa: vista la completezza del sito in Ariel relativo al corso, ho pensato di inserire sul wiki consigli pratici allo studio della materia.
Richiami di algebra lineare
Prima lezione - 2 ottobre
Esempi di spazi vettoriali, reali e complessi con esibizione esplicita di basi:
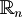 : operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori
: operazioni algebriche e loro interpretazione geometrica; verifica concreta dell'indipendenza di k vettori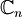 come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n
come spazio vettoriale complesso di dimensione n e come spazio vettoriale reale di dimensione 2n![P_{n}[x]](/images/math/9/6/7/967b23d5681e09247109d9acce668c46.png) : polinomi di grado minore od uguale a n nella variabile x
: polinomi di grado minore od uguale a n nella variabile x- matrici n x m
- funzioni da
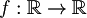 come esempio di spazio di dimensione infinita
come esempio di spazio di dimensione infinita
Sottospazi vettoriali:
- definizione di sottospazio e chiusura rispetto alle operazioni vettoriali
- esempi concreti di verifica con calcolo della dimensione e deteminazione di una base
La lezione si è occupata prevalentemente del paragrafo 2.2 delle dispense di P. Favro ed A. Zucco che si trovano sul sito del corso.
In particolar modo è importante sapere verificare se
- dati un insieme di vettori essi siano o meno indipendenti;
- dato un sottoinsieme di uno spazio vettoriale esso sia o meno un sottospazio vettoriale;
Seconda lezione - 3 ottobre
Somma di sottospazi Y,Z di X
- l'unione Y∪Z non e' in generale un sottospazio di X
- Y+Z come minimo sottospazio contenente Y∪Z
- consistenza di Y∩Z ed unicita' della decomposizione
- somma diretta di sottospazi
Per questa parte si può fare sempre riferimento al paragrafo 2.2, in particolare a quanto scritto nelle pagine 15-16.
Enti lineari in 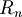
- definizione parametrica di retta
- equazione cartesiana di una retta nel piano
- equazione cartesiana di un piano in
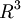
- equazione cartesiana di una retta in
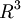 : non unicita'.
: non unicita'.
Fare riferimento a quanto scritto nei paragrafi 3.1 e 3.2. Per quanto riguarda l'equazione del piano in 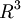 [1].
[1].
Terza lezione - 4 ottobre
Enti lineari in 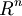 :
:
- definizione parametrica di piano k-dimensionale
- iperpiano = piano di codimensione 1
- esempio di iperpiano in
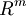 e determinazione della sua equzione cartesiana
e determinazione della sua equzione cartesiana
Operatori lineari:
- definizione ed esempi concreti di verifica
- esempio: sia
- Vogliamo sapere se la funzione B è una mappa lineare o meno; dobbiamo quindi vedere se rispetta l'additività e l'omogeneità.
- Testiamo la seconda nel seguente modo:
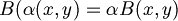 dove
dove 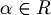
- Poichè non vale l'uguaglianza possiamo concludere che B non è una mappa lineare.
- Vediamo invece un caso in cui lo è:
- Testiamo l'omogeneità
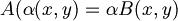 dove
dove 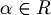
- L'uguaglianza è vera; testiamo ora l'additività:
- Poichè l'uguaglianza è vera, possiamo dice che A è una mappa lineare dallo spazio vettoriale
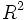 allo spazio vettoriale
allo spazio vettoriale 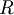
- coniugio nel campo complesso C: R-lineare ma non C-lineare
- L'additività vale in ogni caso:
- Mentre l'omogeneità vale solo se
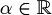
- Infatti se
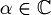 avremmo:
avremmo:
- matrice associata al coniugio, rispetto alla base reale {1, i}
- matrice associata al coniugio, rispetto alla base reale {1, 1+i}
Matrici associate ad un operatore lineare A : X → Y
Gli argomenti trattati da qui in poi sono spiegati chiaramente al paragrafo 2.8 per libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Quarta lezione - 5 ottobre
Operatori astratti A:X→Y
![[x]_{V}](/images/math/6/d/c/6dc5a52d1f4c46d62398dc30d1883ff1.png) vettore delle componenti di x rispetto alla base V
vettore delle componenti di x rispetto alla base V- matrice
![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) associata ad A rispetto alle basi V in X e W in Y
associata ad A rispetto alle basi V in X e W in Y - ricostruzione dell'azione di A a partire dalla matrice associata:
![[Ax]_{W}=[A]_{{WV}}[x]_{V}](/images/math/d/b/a/dba0cf3930f2b34e075a988c44139744.png)
- matrice
![[I]_{{V_{1}V_{2}}}](/images/math/7/7/8/7785d29132b404b44941ce1fb8d09729.png) associata all'indentita': matrice del cambio di base
associata all'indentita': matrice del cambio di base - cambio delle basi ed effetto sulla matrice associata:
![[A]_{{W_{2}V_{2}}}=[I]_{{W_{2}W_{1}}}[A]_{{W_{1}V_{1}}}[I]_{{V_{1}V_{2}}}](/images/math/c/7/d/c7dea2a1cd1599413989c7e2e066ceba.png)
Operatori lineari 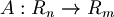
- base canonica E
- proprieta' notevole della base canonica
![[x]_{E}=x](/images/math/7/f/0/7f0b02758335d84c2f675d0617615993.png)
- azione dell'operatore nelle basi canoniche:
![Ax=[Ax]_{E}=[A]_{{EE}}[x]_{E}=[A]_{{EE}}x](/images/math/8/e/e/8eed802d2144a10f507acc87054b18df.png)
- identificazione operatore-matrice nelle basi canoniche:
![A=[A]_{{EE}}](/images/math/b/0/8/b08e44fb3e06e97ad70f9250cfa40fbb.png)
- esempi di calcolo della matrice rappresentativa in basi non canoniche
Tutti i punti sopra citati sono trattati nel paragrafo 2.8 del libro "Linear Algebra Done Wrong" di cui trovate il link sul sito del corso.
- immagine di un operatore e sua dimensione: rango di ogni matrice rappresentativa
- sia
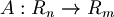 una qualsiasi mappa lineare, l'immagine di A è:
una qualsiasi mappa lineare, l'immagine di A è: 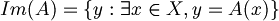
- La dimensione di
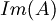 è data dal rango della matrice rappresentativa di A:
è data dal rango della matrice rappresentativa di A: ![[A]_{{WV}}](/images/math/b/0/8/b081464ee0ce4562be67a879cd81e2ca.png) , dove V è base di
, dove V è base di 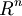 e W è base di
e W è base di 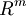
- nucleo di un operatore e sua dimensione: numero colonne - rango di ogni matrice rappresentativa
- Il nucleo di un operatore (anche detto kernel) è:
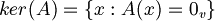 , dove con
, dove con 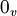 intendo il vettore nullo del codominio.
intendo il vettore nullo del codominio.
- caratterizzazione iniettivita'\suriettivita' tramite rango matrice rappresentativa
- Sia V uno spazio vettoriale e A un'applicazione lineare, allora dim(ker(A)) + dim((Im(A)) = dim(V);
- La funzione A è iniettiva se dim(Ker(A)) = 0, ovvero se
 ;
; - La funzione A è suriettiva se dim(Im(A)) = dim(W). Ricordo che V è una base del dominio e W del codominio.
- il caso speciale dominio=codominio: iniettivita' equivalente a suriettivita'.
Soluzione esercizi
1.1a) Dire se 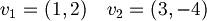 sono linearmente indipendenti.
sono linearmente indipendenti.
- In generale, diciamo che n vettori
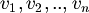 sono linearmente indipendenti quando
sono linearmente indipendenti quando
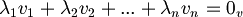 solo quando
solo quando
- (
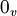 è il vettore nullo,
è il vettore nullo, 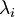 sono i coefficienti)
sono i coefficienti)
- Per verificare questo abbiamo principalmente due modi:
- I vettori vengono riscritti come prodotto delle basi, in questo caso canoniche, quindi

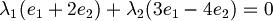
Raccogliamo le due basi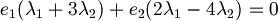
Mettiamo le due equazioni a sistema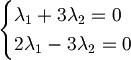
Risolvendolo si trova che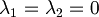 quindi possiamo concludere che sono linearmente indipendenti.
quindi possiamo concludere che sono linearmente indipendenti. - Un metodo molto più veloce è fare la matrice dei due vettori:
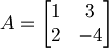
che corrisponde alla matrice dei coefficienti del sistema appena sopra
Se verifichiamo che il determinante di questa matrice è diverso da zero allora possiamo dire che la soluzione del sistema è la soluzione banale (questa proprietà del determinante vale solo per le matrici quadrate), ovvero tutti i lambda a zero.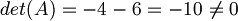
Anche in questo modo possiamo concludere che i vettori sono linearmente indipendenti.
1.1b) Lo stesso per i vettori 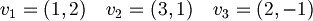
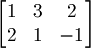
- Poichè formano una matrice 2 x 3, possiamo già dire che non sono indipendenti perchè il rango massimo è 2, e il rango è il massimo numero di vettori linearmente indipendenti.
- Risposta: no, non sono linearmente indipendenti.
1.2) Non sono linearmente indipendenti poichè il determinante è 0.
1.3) Sono linearmente indipendenti poichè il determinante è diverso da 0.
1.4) Boh
1.5) Essendo in un campo di 3 dimensioni, basta che i tre vettori siano linearmente indipendenti infatti, il numero di dimensioni ci dice il massimo numero di vettori linearmente indipendenti tra di loro. E' quindi una base.
1.7) Un sottoinsieme di uno spazio vettoriale è tale se è a sua volta un sottospazio, ovvero le operazioni di somma è prodotto per scalare sono chiuse (il loro risultato appartiene al sottospazio).
- Somma:
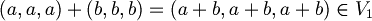
Prodotto: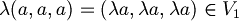
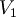 è un sottospazio di
è un sottospazio di 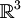
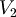 è un sottospazio di
è un sottospazio di 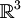
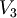 è un sottospazio di
è un sottospazio di 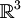
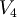 non è un sottospazio di
non è un sottospazio di 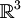
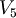 non è un sottospazio di
non è un sottospazio di 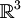
1.15) Le rette 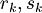 sono definite come l'intersezione dei piani le cui equazioni sono nei sistemi.
sono definite come l'intersezione dei piani le cui equazioni sono nei sistemi.
- Dobbiamo trovare il punto P in cui si incontrano, al variare di k. Per fare ciò dobbiamo trovare la soluzione al sistema unito.
- Uniamo i sistemi:
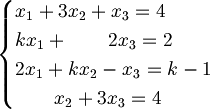
- Riduciamolo ad un sistema di 2 equazioni in 2 incognite:
- Sommiamo la prima riga alla terza;
- Moltiplichiamo la seconda per
 e sottraiamo la quarta riga:
e sottraiamo la quarta riga:
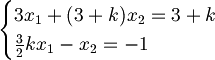
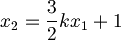 Sostituendo nella prima, dopo alcune semplificazioni, si arriva a
Sostituendo nella prima, dopo alcune semplificazioni, si arriva a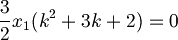
- Se il trinomio in k si annulla (questo accade per
 , l'equazione è vera per qualsiasi
, l'equazione è vera per qualsiasi 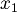 : non si tratta quindi di un punto e non ha senso studiarlo.
: non si tratta quindi di un punto e non ha senso studiarlo. - Se invece k è diverso da quei valori, l'equazione è vera solo per
 . Da questo è facile trovare che
. Da questo è facile trovare che 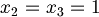
- Il punto P in cui si incontrano le rette sarà

- L'esercizio chiede inoltre di trovare l'equazione della retta
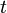 passante per l'origine e
passante per l'origine e 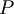 :
: 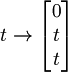 di cui si può anche trovare l'equazione cartesiana:
di cui si può anche trovare l'equazione cartesiana: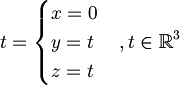
- e togliendo t
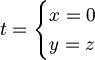
Spazi euclidei e calcolo vettoriale
Quinta lezione - 9 ottobre
Norma in spazi vettoriali reali
- La norma di
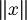 è la distanza del punto x dal punto 0.
è la distanza del punto x dal punto 0.
Norma Euclidea 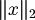 in
in 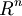 e sua giustificazione tramite teorema di Pitagora
e sua giustificazione tramite teorema di Pitagora
- Sia
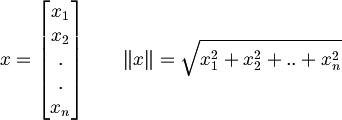
- In
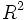 è il noto teorema di pitagora:
è il noto teorema di pitagora: 
Proprieta' della norma Euclidea:
- positivita' ed annullamento
- positiva omogeneita'
- disuguaglianza triangolare (senza dimostrazione, per il momento)
Assiomatizzazione del concetto di norma: Una norma è una qualsiasi funzione che rispetta le precedenti proprietà. Per distinguere le differenti norme si pone un pedice dopo il suo simbolo.
La norma euclidea ha pedice 2; tuttavia, durante il corso, non si porrà tale pedice.
Esempi di norme differenti in 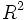
- norma del tassista
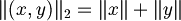
- norma infinito
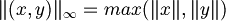
- geometria delle relative palle unitarie
Esempi di norme in altri spazi:
- norma Euclidea negli spazi di matrici
- norma del sup nello spazio di funzioni limitate
Prodotto scalare in uno spazio reale
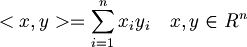
E' quindi una funzione che associa a due vettori un elemento del campo.
Nozione di ortogonalita' tra vettori di 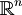 nella norma Euclidea:
nella norma Euclidea:
- Due vettori sono ortogonali se e solo se
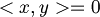
- caratterizzazione ortogonalita' tramite teorema di Pitagora
- Il teorema di Pitagora afferma che quando si tratta di triangoli rettangoli, ovvero con due lati ortogonali, si ha che
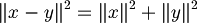 (teorema di pitagora riscritto in maniera diversa)
(teorema di pitagora riscritto in maniera diversa)- ma poichè
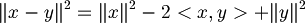
- concludiamo che questo accade solo quando
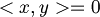
- espressione in componenti dell'ortogonalita'
- definzione di prodotto scalare Euclideo
- ricostruzione norma Euclidea a partire dal prodotto scalare Euclideo
Proprieta' del prodotto scalare < , > e sua assiomatizzazione:
- simmetria: <x,y>=<y,x> per ogni x,y
- bilinearita' che nella prima componente si scrive; <ax+bz,y>=a<x,y>+b<z,y> per ogni scalare a,b ed ogni x,z,y
- positivita' ed annullamento: x≠0 implica <x,x>>0
Norma associata ad un prodotto scalare:
- definizione ||x||2=<x,x>
- omogeneita', positivita' ed annullamento della norma
- disuguagliqanza di Schwarz e suo utlizzo per la disuguaglianza triangolare della norma
Non tutte le norme derivano da un prodototo scalare
- identita' del parallelogrammo e sue conseguenze
- il caso della norma del tassista
Sesta lezione - 10 ottobre
Basi ortonormali
- Una base ortonormale è formata da vettori ortogonali tra loro e tutti di norma 1.
Relazioni tra ortogonalita' ed indipendenza:
- un insieme di vettori non nulli ed ortogonali a coppie e' lineramente indipendente (infatti il vettore nullo è ortogonale a qualsiasi vettore ma ne è anche dipendente)
- viceversa ovviamente falso
Definizione ed esempi di basi ortonormali, tra cui la base canonica di 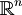 con prodotto scalare Euclideo
con prodotto scalare Euclideo
Decomposizione di un vettore lungo una base ortonormale:
- calcolo delle componenti
- calcolo della norma
Distanza minima e proiezione ortogonale in dimensione 1
Problema: dato V=Rv ed x∈V determinare per la minima distanza di x da V
- determinare per quale t la funzione f(t)=||x-tv||2 e' minima
- risposta: t*=<x,v>/||v||2
- x*=t*v piede della perpendicolare a V condotta da x
- caratterizzazione geometrica x*: <x-x*,v>=0
- linearita' della mappa x→x*: rango, immagine e nucleo
- Data una base unidimensionale
 e un vettore
e un vettore 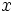 di cui si vuole trovare la proiezione ortogonale
di cui si vuole trovare la proiezione ortogonale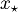
- Sappiamo intuitivamente che
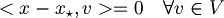 però devo trovare
però devo trovare 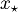
- Per far ciò, data la retta
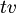 cerco
cerco 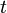 tale che la distanza da
tale che la distanza da 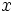 sia minima, quindi
sia minima, quindi 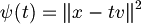 è la funzione che descrive il quadrato della distanza,
è la funzione che descrive il quadrato della distanza,- Ne studio la derivata e vedo che è uguale a zero quando
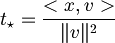
- di conseguenza
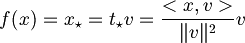
- Dimostro che la minima distanza e la proiezione ortogonale coincidono
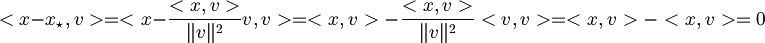
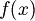 è lineare poichè è lineare il prodotto scalare.
è lineare poichè è lineare il prodotto scalare.
Enunciato e dimostrazione disuguaglianza di Schwarz, con caratterizzazione uguaglianza
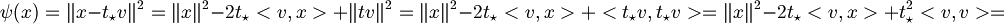
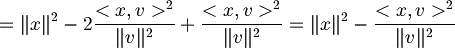
- Ciò dimostra la disuguaglianza di Schwarz infatti
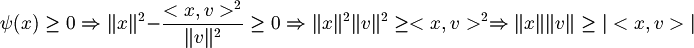
- L'uguaglianza si verifica quando
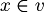
Versione geometrica del prodotto scalare:
- nel Rn Euclideo, dalla trigonometria elementare <x,v>=||x||||v||cos(θ)
- nel caso generale, la formula precedente definisce θ
Settima lezione - 12 ottobre
Distanza minima da un sottospazio V⊂X di dimensione qualunque
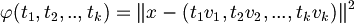 (quadrato della distanza)
(quadrato della distanza)- Studiare il minimo di questa funzione è molto complesso quindi
Risoluzione geometrica, ovvero proiezione ortogonale di x∈X su V:
- definizione come x*∈V tale che ⟨x-x*,v⟩=0 per ogni v∈V
- dimostrazione unicita' di x*
Dimostriamo per assurdo che esista un altro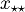
Allora sarebbero vere le due equazioni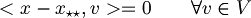
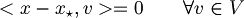
di conseguenza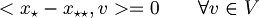
ma poichè deve essere vero per ogni v, scegliamo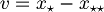
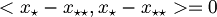
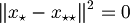 ma due punti a distanza zero coincidono! Quindi
ma due punti a distanza zero coincidono! Quindi 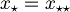
- dimostrazione costruttiva esistenza di x* tramite scelta di una base v1, ..., vk per il sottospazio V
- matrice di Gram associata a v1, ..., vk
- esempio concreto di inversione della matricie di Gram e calcolo di x*
Proprieta' generali della proiezione ortogonale PV su V:
- operatore lineare X→X
- immagine = V
- nucleo = tutti e soli i vettori di X che sono ortogonali a V
- PVPV=PV
Studio della matrice di Gram
Definizione:
- v1, ..., vk∈X vettori assegnati
- matrice G=G(v1, ..., vk) definita tramite Gij=⟨vi,vj⟩
- matrice quadrata simmetrica di dimensione k
Teorema: G invertibile se e solo se i vettori v1, ..., vk∈X sono linearmente indipendenti
Passi chiave della dimostrazione:
- u=λ1v1+...+λkvk e w=μ1v1+...+μkvk generici elementi di V
- λ=(λ1,...,λk) e μ=(μ1,...,μk) elementi di Rk
- vale formula di calcolo ⟨w,u⟩=⟨μ,Gλ⟩ dove l'ultimo prodotto scalare e' quello Euclideo standard di Rk
- dedurne che u=0 equivale a Gλ=0
- invertibilita' di G equivalente alla iniettivita' dell'operatore associato (base canonica)
Osservazioni:
- quando i vettori v1, ..., vk sono ortonormali, la matrice di Gram e' l'identita'
- metodo molto conveniente per valutare indipendenza lineare quando k<dim(X)