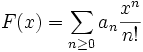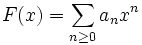Differenze tra le versioni di "Teoria dei grafi/2006-2007"
m (→Diario del corso) |
(Lezione del 16 Ottobre 2006) |
||
| (5 versioni intermedie di uno stesso utente non sono mostrate) | |||
| Riga 62: | Riga 62: | ||
** [[:it:Funzione_generatrice#Funzione_generatrice_esponenziale|funzione generatrice esponenziale]]: <math>F(x)=\sum_{n \ge 0}a_n \frac{x^n}{n!}</math> | ** [[:it:Funzione_generatrice#Funzione_generatrice_esponenziale|funzione generatrice esponenziale]]: <math>F(x)=\sum_{n \ge 0}a_n \frac{x^n}{n!}</math> | ||
** [[:it:Funzione_generatrice#Funzione_generatrice_ordinaria|funzione generatrice ordinaria o geometrica]]: <math>F(x)=\sum_{n \ge 0}a_n x^n</math> | ** [[:it:Funzione_generatrice#Funzione_generatrice_ordinaria|funzione generatrice ordinaria o geometrica]]: <math>F(x)=\sum_{n \ge 0}a_n x^n</math> | ||
| + | |||
| + | === Lezione del 6 Ottobre 2006 === | ||
| + | * polinomi: relazioni tra base, radici e coefficienti | ||
| + | * [[wikipedia:Symmetric_function|funzioni simmetriche]] | ||
| + | ** [[wikipedia:Elementary_symmetric_polynomial|elementari]] | ||
| + | ** omogenee complete | ||
| + | * successione persistente di polinomi | ||
| + | |||
| + | === Lezione del 9 Ottobre 2006 === | ||
| + | * [[:it:Relazione|relazione]] | ||
| + | * [[::it:Relazione di equivalenza|relazione di equivalenza]] | ||
| + | * [[:it:Relazione d'ordine|relazione d'ordine]] parziale | ||
| + | ** [[:it:Diagramma di Hasse|diagramma di Hasse]] | ||
| + | ** insieme parzialmente ordinato (IPO o POSet) | ||
| + | ** [[:it:Funzione_di_Mobius|funzione di Möbius]] | ||
| + | |||
| + | === Lezione del 12 Ottobre 2006 === | ||
| + | * minima limitazione superiore e massima limitazione inferiore di un IPO | ||
| + | * reticolo | ||
| + | * reticolo di partizioni | ||
| + | * polinomio caratteristico di un reticolo | ||
| + | * teoria delle inversioni di Möbius | ||
| + | |||
| + | === Lezione del 13 Ottobre 2006 === | ||
| + | * funzioni tra alberi radicati open maps (preservano ordine e downset) | ||
| + | * mappatura tra catene | ||
| + | * mappatura da alberi a catene | ||
| + | * mappatura da catene ad alberi | ||
| + | * leaf theorem | ||
| + | |||
| + | === Lezione del 16 Ottobre 2006 === | ||
| + | * partizioni di un albero | ||
| + | * ordinamento dei blocchi in una partizione | ||
| + | * albero dei blocchi | ||
| + | * numero funzioni totali e di iniezioni tra due insiemi | ||
Versione attuale delle 12:24, 17 ott 2006
Informazioni generali
Teoria dei grafi è un insegnamento complementare dei Corsi di Laurea del DSI/DICo.
Docente
Orari delle lezioni
- Lunedì 17.30 - 19.30
- Giovedì 17.30 - 19.30
- Venerdì 16.30 - 18.30
in Auletta 5 (via Comelico).
Orario di ricevimento studenti
Lunedì 12.00 - 14.00 in P117.
Sito del corso
http://homes.dico.unimi.it/~dantona/tg/
Materiale didattico
- "Introduzione alla matematica discreta" del docente (disponibile in biblioteca)
Modalità d'esame
- Orale o tesina su uno degli argomenti del corso
Diario del corso
Lezione del 2 Ottobre 2006
- introduzione al corso e alla combinatoria
Lezione del 5 Ottobre 2006
- partizione di un insieme
- numeri di Stirling di seconda specie S(n,k):
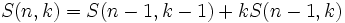
- funzione generatrice di una successione di numeri
Lezione del 6 Ottobre 2006
- polinomi: relazioni tra base, radici e coefficienti
- funzioni simmetriche
- elementari
- omogenee complete
- successione persistente di polinomi
Lezione del 9 Ottobre 2006
- relazione
- [[::it:Relazione di equivalenza|relazione di equivalenza]]
- relazione d'ordine parziale
- diagramma di Hasse
- insieme parzialmente ordinato (IPO o POSet)
- funzione di Möbius
Lezione del 12 Ottobre 2006
- minima limitazione superiore e massima limitazione inferiore di un IPO
- reticolo
- reticolo di partizioni
- polinomio caratteristico di un reticolo
- teoria delle inversioni di Möbius
Lezione del 13 Ottobre 2006
- funzioni tra alberi radicati open maps (preservano ordine e downset)
- mappatura tra catene
- mappatura da alberi a catene
- mappatura da catene ad alberi
- leaf theorem
Lezione del 16 Ottobre 2006
- partizioni di un albero
- ordinamento dei blocchi in una partizione
- albero dei blocchi
- numero funzioni totali e di iniezioni tra due insiemi