Differenze tra le versioni di "Calcolo probabilità e statistica matematica/Esami/2008-01-10"
(→Testo soluzione) |
(→Testo soluzione) |
||
| Riga 56: | Riga 56: | ||
<math> {n \cdot p} = 10 \cdot {1 \over 30} = {1 \over 3}</math> | <math> {n \cdot p} = 10 \cdot {1 \over 30} = {1 \over 3}</math> | ||
| − | <math> {(1-p)^n} = (1 - {1 \over 30})^10 = (29 \over 30)^10 = 7,12 \cdot 10^ | + | <math> {(1-p)^n} = (1 - {1 \over 30})^{10} = ({29 \over 30})^{10} = 7,12 \cdot 10^{-1}</math> |
** c) <math>n=10^9, p={1 \over {3 \cdot 10^9}}</math> | ** c) <math>n=10^9, p={1 \over {3 \cdot 10^9}}</math> | ||
| Riga 62: | Riga 62: | ||
<math> {n \cdot p} = 10^9 \cdot {1 \over {3 \cdot 10^9}} = {1 \over 3}</math> | <math> {n \cdot p} = 10^9 \cdot {1 \over {3 \cdot 10^9}} = {1 \over 3}</math> | ||
| − | <math> {(1-p)^n} = (1 - {1 \over {3 \cdot 10^9}})^10^9 = 7,17 \cdot 10^ | + | <math> {(1-p)^n} = (1 - {1 \over {3 \cdot 10^9}})^{10^9} = 7,17 \cdot 10^{-1}</math> |
| − | ** d) <math>n=10^23, p={1 \over {3 \cdot 10^23}}</math> | + | ** d) <math>n=10^{23}, p={1 \over {3 \cdot 10^{23}}}</math> |
| − | <math> {n \cdot p} = 10^23 \cdot {1 \over {3 \cdot 10^23}} = {1 \over 3}</math> | + | <math> {n \cdot p} = 10^{23} \cdot {1 \over {3 \cdot 10^{23}}} = {1 \over 3}</math> |
| − | <math> {(1-p)^n} = (1 - {1 \over {3 \cdot 10^23}})^10^23 \approx e^{-{1 \over 3}} = 7,17 \cdot 10^(-1) </math> | + | <math> {(1-p)^n} = (1 - {1 \over {3 \cdot 10^{23}}})^{10^{23}} \approx e^{-{1 \over 3}} = 7,17 \cdot 10^(-1) </math> |
Versione delle 13:34, 12 gen 2008
Indice
Tema d'esame del 10-01-2007
Problemi modellati
- Generatore di impulsi
Distribuzioni
- Bernoulli
- Binomiale
- Geometrica
Immagine testo
Testo soluzione
ESERCIZIO I
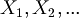 sono v.c. bernoulliane indipendenti e identicamente distribuite
sono v.c. bernoulliane indipendenti e identicamente distribuite
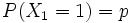 con
con 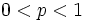
quindi 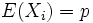
- punto 1)
per la linearita' del valore atteso:
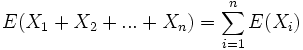
e visto che sono identicamente distribuite:
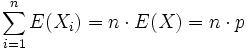
- punto 2)
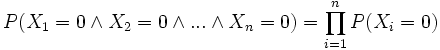
visto che
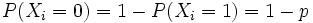
e che le X sono indipendenti e identicamente distribuite:
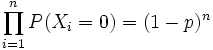
- punto 3)
dal punto precedente abbiamo che:
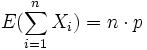
e che:
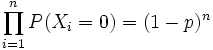
- a)
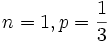
- a)
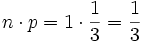
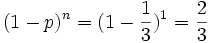
- b)
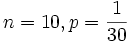
- b)
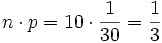
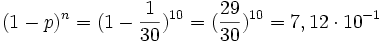
- c)
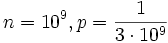
- c)
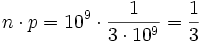
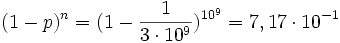
- d)
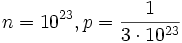
- d)
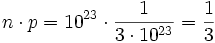
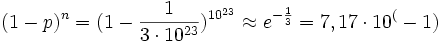
ESERCIZIO II
- punto 1)
- punto 2)
- punto 3)
- punto 4)
ESERCIZIO III
- punto 1)
- punto 2)
- punto 3)
- punto 4)
- punto 5)
- punto 6)
Domande orale
--
