Differenze tra le versioni di "Calcolo probabilità e statistica matematica/Esami/2008-01-10"
(→Testo soluzione) |
(→Testo soluzione) |
||
| Riga 76: | Riga 76: | ||
<math>X_1, X_2, ...</math> sono impulsi BINARI, quindi distribuiti secondo Bernoulli | <math>X_1, X_2, ...</math> sono impulsi BINARI, quindi distribuiti secondo Bernoulli | ||
| − | (NB: Il fatto che i valori che l'impulso puo' assumere siano 1 e -1 non e' rilevante nel nostro caso, potrebbero benissimo essere 2 e 3, quello che conta NON e' QUALI ma '''QUANTI''' valori puo' assumere l'impulso, cioe' '''2''' valori) | + | (NB: Il fatto che i valori che l'impulso puo' assumere siano '1' e '-1' non e' rilevante nel nostro caso, potrebbero benissimo essere '2' e '3' oppure 'a' e 'b', quello che conta qui NON e' QUALI ma '''QUANTI''' valori puo' assumere l'impulso, cioe' '''2''' valori) |
* punto 1) | * punto 1) | ||
| Riga 88: | Riga 88: | ||
<math>S_{m(x)} = </math> "numero di segnali '1' emessi nei primi <math>x</math> secondi" | <math>S_{m(x)} = </math> "numero di segnali '1' emessi nei primi <math>x</math> secondi" | ||
| − | <math>S_{m(x)}</math> conta il numero di impulsi=1, ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri <math>p</math> e <math>\lfloor x \rfloor</math>. | + | <math>S_{m(x)}</math> conta il numero di impulsi='1', ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri <math>p</math> e <math>\lfloor x \rfloor</math>. |
* punto 3) | * punto 3) | ||
| + | G = "numero di secondi passati al primo segnale '1'" | ||
* punto 4) | * punto 4) | ||
Versione delle 14:08, 12 gen 2008
Indice
Tema d'esame del 10-01-2007
Problemi modellati
- Generatore di impulsi
Distribuzioni
- Bernoulli
- Binomiale
- Geometrica
Immagine testo
Testo soluzione
ESERCIZIO I
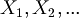 sono v.c. bernoulliane indipendenti e identicamente distribuite
sono v.c. bernoulliane indipendenti e identicamente distribuite
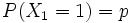 con
con 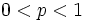
quindi 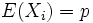
- punto 1)
per la linearita' del valore atteso:
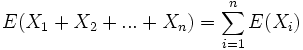
e visto che sono identicamente distribuite:
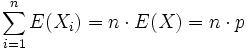
- punto 2)
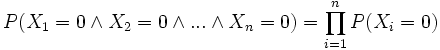
visto che
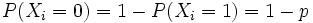
e che le X sono indipendenti e identicamente distribuite:
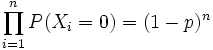
- punto 3)
dal punto precedente abbiamo che:
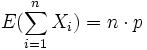
e che:
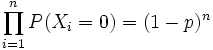
- a)
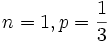
- a)
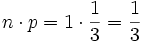
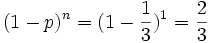
- b)
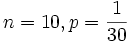
- b)
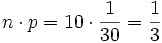
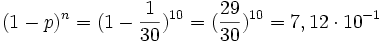
- c)
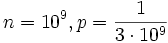
- c)
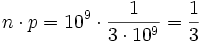
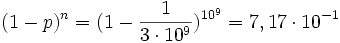
- d)
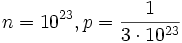
- d)
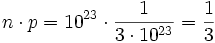
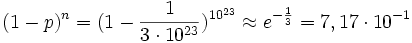
ESERCIZIO II
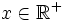
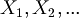 sono impulsi BINARI, quindi distribuiti secondo Bernoulli
sono impulsi BINARI, quindi distribuiti secondo Bernoulli
(NB: Il fatto che i valori che l'impulso puo' assumere siano '1' e '-1' non e' rilevante nel nostro caso, potrebbero benissimo essere '2' e '3' oppure 'a' e 'b', quello che conta qui NON e' QUALI ma QUANTI valori puo' assumere l'impulso, cioe' 2 valori)
- punto 1)
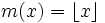
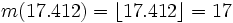
- punto 2)
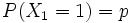
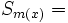 "numero di segnali '1' emessi nei primi
"numero di segnali '1' emessi nei primi 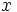 secondi"
secondi"
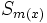 conta il numero di impulsi='1', ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri
conta il numero di impulsi='1', ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri 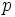 e
e 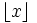 .
.
- punto 3)
G = "numero di secondi passati al primo segnale '1'"
- punto 4)
ESERCIZIO III
- punto 1)
- punto 2)
- punto 3)
- punto 4)
- punto 5)
- punto 6)
Domande orale
--
