Differenze tra le versioni di "Calcolo probabilità e statistica matematica/Esami/2008-01-10"
(→Testo soluzione) |
(→Testo soluzione) |
||
| Riga 125: | Riga 125: | ||
ESERCIZIO III | ESERCIZIO III | ||
| + | <math> r \in \N^+</math> conta il numero di impulsi al secondo | ||
| + | |||
| + | <math>X_1 = </math> primo segnale emesso al tempo <math>t={1 \over r}</math> | ||
| + | |||
| + | <math>X_2 = </math> secondo segnale emesso al tempo <math>t={2 \over r}</math> | ||
| + | |||
| + | <math>X_3 = </math> terzo segnale emesso al tempo <math>t={3 \over r}</math> | ||
| + | |||
| + | <math>\vdots</math> | ||
| + | |||
* punto 1) | * punto 1) | ||
| + | |||
| + | <math>x \in \R^+ </math> | ||
| + | |||
| + | <math>m(r, x) = </math> numero di impulsi nei primi <math>x</math> secondi = numero impulsi al secondo * numero di secondi = <math>r \cdot x</math>. Visto che sto contanto impulsi, e non posso avere frazioni di impulso, arrotondo questo valore finale al maggiore intero positivo inferiore a <math>r \cdot x</math>. | ||
| + | |||
| + | <math>m(r, x) = \lfloor r \cdot x \rfloor</math> | ||
| + | |||
| + | <math>m(3, 17.412) = \lfloor 3 \cdot 17.412 \rfloor = \lfloor 52.236 \rfloor = 52</math> | ||
* punto 2) | * punto 2) | ||
| + | Le X sono bernoulliane indipendenti e identicamente distribuite con <math>P(X_1=1) = p</math> | ||
* punto 3) | * punto 3) | ||
Versione delle 15:21, 12 gen 2008
Indice
Tema d'esame del 10-01-2007
Problemi modellati
- Generatore di impulsi
Distribuzioni
- Bernoulli
- Binomiale
- Geometrica
Immagine testo
Testo soluzione
ESERCIZIO I
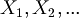 sono v.c. bernoulliane indipendenti e identicamente distribuite
sono v.c. bernoulliane indipendenti e identicamente distribuite
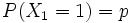 con
con 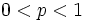
quindi 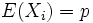
- punto 1)
per la linearita' del valore atteso:
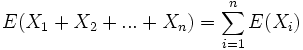
e visto che sono identicamente distribuite:
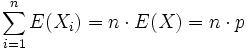
- punto 2)
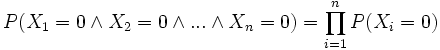
visto che
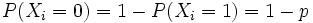
e che le X sono indipendenti e identicamente distribuite:
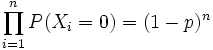
- punto 3)
dal punto precedente abbiamo che:
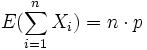
e che:
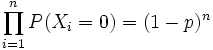
- a)
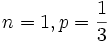
- a)
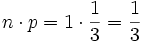
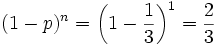
- b)
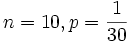
- b)
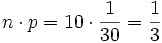
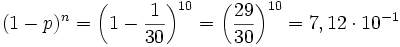
- c)
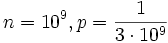
- c)
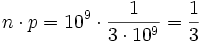
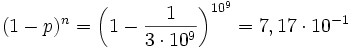
- d)
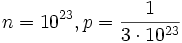
- d)
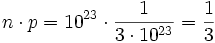
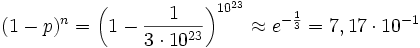
ESERCIZIO II
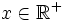
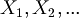 sono impulsi BINARI, quindi distribuiti secondo Bernoulli
sono impulsi BINARI, quindi distribuiti secondo Bernoulli
(NB: Il fatto che i valori che l'impulso puo' assumere siano '1' e '-1' non e' rilevante nel nostro caso, potrebbero benissimo essere '2' e '3' oppure 'a' e 'b', quello che conta qui NON e' QUALI ma QUANTI valori puo' assumere l'impulso, cioe' 2 valori)
- punto 1)
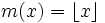
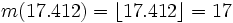
- punto 2)
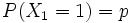
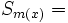 "numero di segnali '1' emessi nei primi
"numero di segnali '1' emessi nei primi 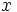 secondi"
secondi"
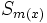 conta il numero di impulsi='1', ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri
conta il numero di impulsi='1', ovvero conta i "successi"; quindi e' distribuita come una BINOMIALE di parametri 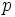 e
e 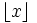 .
.
- punto 3)
G = "numero di secondi passati al primo segnale '1'"
quindi G e' distribuita come una GEOMETRICA.
- a)
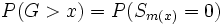
La probabilita' che il primo impulso '1' avvenga DOPO il tempo 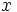 equivale a dire che tutti gli impulsi fino al tempo
equivale a dire che tutti gli impulsi fino al tempo 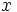 son stati '-1', ovvero insuccessi; quindi devo sommare
son stati '-1', ovvero insuccessi; quindi devo sommare 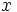 insuccessi.
insuccessi.
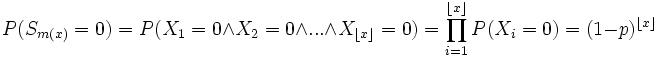
Quindi:
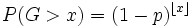
- b)
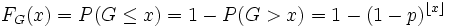
- punto 4)
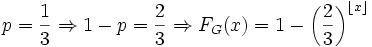
NB: Il disegno qui e' un po' un casino da fare, comunque e' quello che si trova sul libro a pag. 67 (figura 2.2), cambiano solo i valori sulle ordinate:
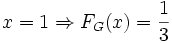
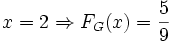
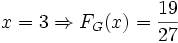
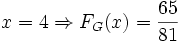

ESERCIZIO III
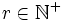 conta il numero di impulsi al secondo
conta il numero di impulsi al secondo
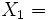 primo segnale emesso al tempo
primo segnale emesso al tempo 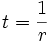
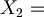 secondo segnale emesso al tempo
secondo segnale emesso al tempo 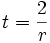
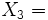 terzo segnale emesso al tempo
terzo segnale emesso al tempo 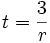

- punto 1)
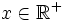
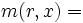 numero di impulsi nei primi
numero di impulsi nei primi 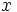 secondi = numero impulsi al secondo * numero di secondi =
secondi = numero impulsi al secondo * numero di secondi =  . Visto che sto contanto impulsi, e non posso avere frazioni di impulso, arrotondo questo valore finale al maggiore intero positivo inferiore a
. Visto che sto contanto impulsi, e non posso avere frazioni di impulso, arrotondo questo valore finale al maggiore intero positivo inferiore a  .
.
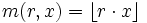
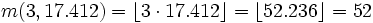
- punto 2)
Le X sono bernoulliane indipendenti e identicamente distribuite con 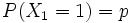
- punto 3)
- punto 4)
- punto 5)
- punto 6)
Domande orale
--
