Differenze tra le versioni di "Metodi probabilistici/2007-2008"
(→Diario del corso) |
|||
| (8 versioni intermedie di 2 utenti non mostrate) | |||
| Riga 8: | Riga 8: | ||
* Ripasso del concetto di funzione di ripartizione | * Ripasso del concetto di funzione di ripartizione | ||
** Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato | ** Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato | ||
| − | * Primo approccio al concetto di funzione misurabile (Sigma-s misurabile, con s semiretta dei Reali) | + | * Primo approccio al concetto di funzione misurabile (<math>\Sigma</math>-s misurabile, con s semiretta dei Reali <math>\mathbb{R}</math>) |
=== Lezione del giorno 7/3/2008 === | === Lezione del giorno 7/3/2008 === | ||
| − | * Recap del modello Kolmogoroviano ( | + | * Recap del modello Kolmogoroviano (<math>\Omega</math>, <math>\Sigma</math>, P) |
* Proprietà delle funzioni di ripartizione | * Proprietà delle funzioni di ripartizione | ||
** Ripasso del concetto di continuità da dx e sx | ** Ripasso del concetto di continuità da dx e sx | ||
| Riga 18: | Riga 18: | ||
** Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo". | ** Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo". | ||
*** Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti". | *** Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti". | ||
| − | ** Parallelismo tra Modello Kolmogoroviano e terna (R, B(R), | + | ** Parallelismo tra Modello Kolmogoroviano e terna (<math>\mathbb{R}</math>, <math>\mathcal{B}</math>(<math>\mathbb{R}</math>), <math>P_X</math>) |
| − | ** Prima citazione degli insieme di Borel | + | ** Prima citazione degli insieme di Borel <math>\mathcal{B}</math>(<math>\mathbb{R}</math>). |
* Ripasso del concetto di esponenziale (con naturale estensione al piano complesso) | * Ripasso del concetto di esponenziale (con naturale estensione al piano complesso) | ||
** Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x) | ** Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x) | ||
*** Ripasso del concetto di derivata come limite del rapporto incrementale | *** Ripasso del concetto di derivata come limite del rapporto incrementale | ||
*** Ricerca di una soluzione tra i polinomi | *** Ricerca di una soluzione tra i polinomi | ||
| − | *** Verifica della soluzione | + | *** Verifica della soluzione <math>\sum_{n=0}^{\infty}{\frac{x^n}{n!}}</math> |
*** Verifica della convergenza della serie | *** Verifica della convergenza della serie | ||
| − | ** Definizione formale del numero di | + | ** Definizione formale del numero di Nepero |
** Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton] | ** Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton] | ||
** Esponenziale di complessi | ** Esponenziale di complessi | ||
*** Legame con funzione seno e coseno | *** Legame con funzione seno e coseno | ||
| + | |||
| + | === Lezione del giorno 10/3/2008 === | ||
| + | * Definizione formale di <math>\pi</math>) (non l'ha fatta però, rivedersela per conto proprio) | ||
| + | * Riprendiamo discorso su F di ripartizione | ||
| + | ** Proprietà F che portano al concetto di "Assenza di memoria" | ||
| + | ** Unicità della soluzione per G(x+y) = G(x)+G(y) --> G(x) = exp (-<math>\nu</math>x) | ||
| + | ** Tempo attesa esponenziale (cfr con legge Poisson) | ||
| + | ** Risoluzione primo esercizio CPSM tema di febb | ||
| + | *** Valutazione della derivata della F di ripartizione (in 0 non è definita, i limiti sono diversi) | ||
| + | * Riflessione sulla derivata in <math>\mathbb{C}</math>; è condizione "inifinitamente" stringente poichè vi sono infiniti limiti da valutare (h varia in tutte le oo direzioni in <math>\mathbb{C}</math>) | ||
| + | ** derivabile in <math>\mathbb{C}\Leftrightarrow</math> sviluppabile in serie di potenze | ||
| + | * Introduciamo valore atteso E() | ||
| + | ** Linearità, E(1) = 1, associatività e commutatività per le v.c. | ||
| + | ** Limitazione di X, |X| <math>\leq</math> c | ||
| + | * Definizione formale dell'algebra sulla quale lavoreremo | ||
| + | ** <math> E(A^2) \geq</math> 0 ( = 0 sse A=0) | ||
| + | **<math>\forall A,B \in \mathbb{A}\ \ \exists b \in \mathbb{R}: E(BA^2) \leq bE(A^2) </math> | ||
| + | * Data la struttura <math>\mathbb{A}</math>, esiste uno spazio di probabilità <math>(\Omega, \Sigma, P)</math> tale che <math>\mathbb{A}</math> è isomorfo alla famiglia delle v.c. limitate definite su <math>\Omega</math>, regolari rispetto a <math>\Sigma</math> | ||
| + | * Valore atteso definito come integrale: | ||
| + | <math>E(A) = \int_\Omega a(\omega)dP = \int_\mathbb{R} x \frac{dF}{dx} dx</math> | ||
| + | dove A <-> a tramite l'isomorfismo sopracitato. | ||
| + | * Accenno alla non commutatività dell'algebra | ||
| + | * [http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.bams/1183526903 Irving Segal - Algebraic Integration Theory] cfr. pag. 430. | ||
| + | |||
| + | === Lezione del giorno 14/3/2008 === | ||
| + | * Variabili casuali né continue né discrete | ||
| + | ** Definizioni di valore atteso e varianza di v.c. generiche (2.6 MGB 75 e 2.9 MGB 78) | ||
| + | ** Rimando a definizione elementare di E(x) da CPSM --> la definizione di varianza dipende dalla definizione di valore atteso. | ||
| + | * Ridefinizione formale del th. di pag 432 articolo Irving Segal | ||
| + | ** Esempi pratici di isomorfismi tra algebre e loro realizzazioni | ||
| + | *** Corpo lanciato che segue traiettoria | ||
| + | *** Distribuzione delle particelle in un gas | ||
| + | * Dimostrazione della disuguaglianza di Tcheb. secondo il th sopracitato. | ||
| + | * Cauchy - Schwarz su v.c. limitate | ||
| + | ** si parte da E((Y-tX)^2) con t <math>\in \mathbb{R}</math> | ||
| + | ** Valutiamo discriminante del polinomio | ||
| + | *** Precisazione sul caso in cui E(x)=0 sse le v.c. sono proporzionali secondo t. | ||
| + | ** Si deduce che per le v.c. dotate di momento secondo <math>\exists E(XY)</math> | ||
| + | * Introduzione allo spazio L^2 | ||
| + | ** Tramite Cauchy-Schwarz deduciamo che L^2 è spazio vettoriale | ||
| + | ** Recap di spazio vettoriale e proprietà delle op definite in esso | ||
| + | ** Definizione di lunghezza , distanza rispetto al valore atteso | ||
| + | ** Relazione tra valore atteso e varianza nello spazio vettoriale | ||
| + | === Lezione del giorno 17/3/2008=== | ||
| + | * IL DIARIO DI QUESTA LEZIONE E' UN PO' APPROSSIMATIVO, DEVO ANCORA CAPIRE BENE LA LEZIONE | ||
| + | * Covarianza (utilizzando cauchy-shwarz) | ||
| + | **Coefficiente di correlazione | ||
| + | * Regressione lineare (dimostrazione analitica, attraverso derivate parziali e determinante della matrice associata al sistema lineare definito - CRAMER) | ||
| + | * Il valore atteso di Z (varibile casuale definita come il polinomio di primo grado della regressione) concide con quello della variabile casuale da "stimare" | ||
| + | * Anticipazione su Tcheb. | ||
| + | === Lezione del giorno 28/3/2008=== | ||
| + | * Rivisitazione del concetto di regressione lineare attraverso inferenze di carattere puramente geometrico..tutti gli argomenti trattati il 17 si rifanno il 28 con un approccio molto più semplice e immediato. | ||
| + | * Primo approccio al concetto di valore atteso condizionato (N.B è una variabile casuale) | ||
| + | * Stima parametrica - stimatori UMVUE | ||
| + | ** Dimostrazione unicità stimatori UMVUE | ||
| + | ** il valore atteso della differenza di due v.c. stimatori UMVUE "=" 0 (nella prossima lezione si puntualizza quell'uguale tra virgolette). | ||
| + | === Lezione del giorno 31/3/2008=== | ||
| + | * Iniziamo la lezione con un caso degenere di stimatore (non riusciamo a trovarne uno per il problema posto). | ||
| + | * Valutiamo la statistica (S+T)/2 e ragioniamo ancora sul concetto di unicità dello stimatore UMVUE. | ||
| + | ** Digressione sul "quasi ovunque". | ||
| + | ** Dimostrazione unicità asttraverso il concetto di Probabilità & tcheb. | ||
| + | ** Digressone sulla norma quadra definita in L2 rispetto alla media campionaria. | ||
| + | * Ritorniamo al compito per introdurre le f. generatrici. | ||
| + | ** E' necessario studiare il dominio della f.generatrice...non è cosi banale. | ||
| + | *** Caso della exp negativo | ||
| + | ** Estensione al piano complesso della f. generatrice. | ||
| + | * Dimostrazione che la distribuzione di Cauchy non segue il th centrale della statistica. Infatti non ammette valore atteso! | ||
Versione attuale delle 10:01, 31 mar 2008
Indice
Diario del corso
Lezione del giorno 3/3/2008
- Introduzione al corso
- Partendo dal concetto di variabile casuale ripasso di:
- Funzione, Relazione, Prodotto Cartesiano
- Ripasso del concetto di funzione di ripartizione
- Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato
- Primo approccio al concetto di funzione misurabile (
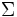 -s misurabile, con s semiretta dei Reali
-s misurabile, con s semiretta dei Reali 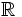 )
)
Lezione del giorno 7/3/2008
- Recap del modello Kolmogoroviano (
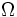 ,
, 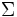 , P)
, P) - Proprietà delle funzioni di ripartizione
- Ripasso del concetto di continuità da dx e sx
- Data una generica F(x) che gode delle tre proprietà (MGB 67-68) questa è una funzione di ripartizione della quale possiamo definire modello Kolmogoroviano. (Vedi MGB 68-2.3)
- Concetto di misurabilità partendo da esempi elementari (da CPSM) con distribuzione uniforme in (a,b]
- Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo".
- Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti".
- Parallelismo tra Modello Kolmogoroviano e terna (
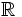 ,
, 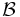 (
(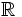 ),
), 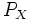 )
) - Prima citazione degli insieme di Borel
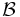 (
(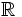 ).
).
- Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo".
- Ripasso del concetto di esponenziale (con naturale estensione al piano complesso)
- Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x)
- Ripasso del concetto di derivata come limite del rapporto incrementale
- Ricerca di una soluzione tra i polinomi
- Verifica della soluzione
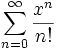
- Verifica della convergenza della serie
- Definizione formale del numero di Nepero
- Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton]
- Esponenziale di complessi
- Legame con funzione seno e coseno
- Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x)
Lezione del giorno 10/3/2008
- Definizione formale di
 ) (non l'ha fatta però, rivedersela per conto proprio)
) (non l'ha fatta però, rivedersela per conto proprio) - Riprendiamo discorso su F di ripartizione
- Proprietà F che portano al concetto di "Assenza di memoria"
- Unicità della soluzione per G(x+y) = G(x)+G(y) --> G(x) = exp (-
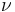 x)
x) - Tempo attesa esponenziale (cfr con legge Poisson)
- Risoluzione primo esercizio CPSM tema di febb
- Valutazione della derivata della F di ripartizione (in 0 non è definita, i limiti sono diversi)
- Riflessione sulla derivata in
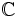 ; è condizione "inifinitamente" stringente poichè vi sono infiniti limiti da valutare (h varia in tutte le oo direzioni in
; è condizione "inifinitamente" stringente poichè vi sono infiniti limiti da valutare (h varia in tutte le oo direzioni in 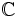 )
)
- derivabile in
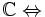 sviluppabile in serie di potenze
sviluppabile in serie di potenze
- derivabile in
- Introduciamo valore atteso E()
- Linearità, E(1) = 1, associatività e commutatività per le v.c.
- Limitazione di X, |X|
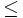 c
c
- Definizione formale dell'algebra sulla quale lavoreremo
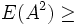 0 ( = 0 sse A=0)
0 ( = 0 sse A=0)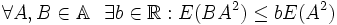
- Data la struttura
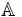 , esiste uno spazio di probabilità
, esiste uno spazio di probabilità 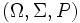 tale che
tale che 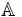 è isomorfo alla famiglia delle v.c. limitate definite su
è isomorfo alla famiglia delle v.c. limitate definite su 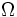 , regolari rispetto a
, regolari rispetto a 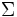
- Valore atteso definito come integrale:
dove A <-> a tramite l'isomorfismo sopracitato.
- Accenno alla non commutatività dell'algebra
- Irving Segal - Algebraic Integration Theory cfr. pag. 430.
Lezione del giorno 14/3/2008
- Variabili casuali né continue né discrete
- Definizioni di valore atteso e varianza di v.c. generiche (2.6 MGB 75 e 2.9 MGB 78)
- Rimando a definizione elementare di E(x) da CPSM --> la definizione di varianza dipende dalla definizione di valore atteso.
- Ridefinizione formale del th. di pag 432 articolo Irving Segal
- Esempi pratici di isomorfismi tra algebre e loro realizzazioni
- Corpo lanciato che segue traiettoria
- Distribuzione delle particelle in un gas
- Esempi pratici di isomorfismi tra algebre e loro realizzazioni
- Dimostrazione della disuguaglianza di Tcheb. secondo il th sopracitato.
- Cauchy - Schwarz su v.c. limitate
- si parte da E((Y-tX)^2) con t
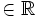
- Valutiamo discriminante del polinomio
- Precisazione sul caso in cui E(x)=0 sse le v.c. sono proporzionali secondo t.
- Si deduce che per le v.c. dotate di momento secondo
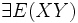
- si parte da E((Y-tX)^2) con t
- Introduzione allo spazio L^2
- Tramite Cauchy-Schwarz deduciamo che L^2 è spazio vettoriale
- Recap di spazio vettoriale e proprietà delle op definite in esso
- Definizione di lunghezza , distanza rispetto al valore atteso
- Relazione tra valore atteso e varianza nello spazio vettoriale
Lezione del giorno 17/3/2008
- IL DIARIO DI QUESTA LEZIONE E' UN PO' APPROSSIMATIVO, DEVO ANCORA CAPIRE BENE LA LEZIONE
- Covarianza (utilizzando cauchy-shwarz)
- Coefficiente di correlazione
- Regressione lineare (dimostrazione analitica, attraverso derivate parziali e determinante della matrice associata al sistema lineare definito - CRAMER)
- Il valore atteso di Z (varibile casuale definita come il polinomio di primo grado della regressione) concide con quello della variabile casuale da "stimare"
- Anticipazione su Tcheb.
Lezione del giorno 28/3/2008
- Rivisitazione del concetto di regressione lineare attraverso inferenze di carattere puramente geometrico..tutti gli argomenti trattati il 17 si rifanno il 28 con un approccio molto più semplice e immediato.
- Primo approccio al concetto di valore atteso condizionato (N.B è una variabile casuale)
- Stima parametrica - stimatori UMVUE
- Dimostrazione unicità stimatori UMVUE
- il valore atteso della differenza di due v.c. stimatori UMVUE "=" 0 (nella prossima lezione si puntualizza quell'uguale tra virgolette).
Lezione del giorno 31/3/2008
- Iniziamo la lezione con un caso degenere di stimatore (non riusciamo a trovarne uno per il problema posto).
- Valutiamo la statistica (S+T)/2 e ragioniamo ancora sul concetto di unicità dello stimatore UMVUE.
- Digressione sul "quasi ovunque".
- Dimostrazione unicità asttraverso il concetto di Probabilità & tcheb.
- Digressone sulla norma quadra definita in L2 rispetto alla media campionaria.
- Ritorniamo al compito per introdurre le f. generatrici.
- E' necessario studiare il dominio della f.generatrice...non è cosi banale.
- Caso della exp negativo
- Estensione al piano complesso della f. generatrice.
- E' necessario studiare il dominio della f.generatrice...non è cosi banale.
- Dimostrazione che la distribuzione di Cauchy non segue il th centrale della statistica. Infatti non ammette valore atteso!