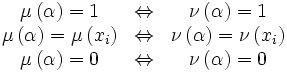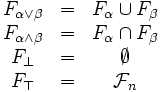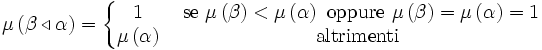Differenze tra le versioni di "Logica fuzzy/2007-2008"

Da WikiDsy.
 
m
 
(28 versioni intermedie di 8 utenti non mostrate)
Riga 1: Riga 1:
−
[[Categoria:Corsi 2006-2007]]
+
[[Categoria:Corsi 2007-2008]]
 
== News ==
 
== News ==
  
 +
ultima lezione: venerdì 11 gennaio
  
 
=== Appelli ===
 
=== Appelli ===
Riga 7: Riga 8:
  
 
== Informazioni generali ==
 
== Informazioni generali ==
 +
 +
=== Sito del corso ===
 +
[http://logicafuzzy.dsi.unimi.it/ logicafuzzy.dsi.unimi.it]
  
 
=== Docenti ===
 
=== Docenti ===
Riga 87: Riga 91:
 
* Assegnamento alle variabili e assegnamento alle formule.
 
* Assegnamento alle variabili e assegnamento alle formule.
 
* Definizioni di tautologia, contraddizione e formula soddisfacibile.
 
* Definizioni di tautologia, contraddizione e formula soddisfacibile.
−
* Esempi di tautologie:
+
* Esempi di tautologie: prelinearità, principio del terzo escluso, ex falso quodlibet, leggi di de Morgan.
−
prelinearità
 
−
principio del terzo escluso
 
−
ex falso quodlibet
 
−
leggi di de Morgan
 
  
 
'''Teoria della dimostrazione (sintassi)'''
 
'''Teoria della dimostrazione (sintassi)'''
Riga 97: Riga 97:
 
* Definizione di dimostrabilità e derivabilità per modus ponens.
 
* Definizione di dimostrabilità e derivabilità per modus ponens.
 
* Teorema di completezza della LPC.
 
* Teorema di completezza della LPC.
 +
 +
 +
=== Lezione di martedì 9/10/2007 ===
 +
 +
'''Logica di Gödel'''
 +
* Definizione di assegnamento alle variabili e alle formule nella LG (e variante di Zadeh).
 +
* Analisi di alcune tautologie della LC che cadono nella LG (legge della doppia negazione, principio del terzo escluso) o restano tautologie (ex falso quodlibet, prelinearità).
 +
* Inclusione stretta dell'insieme delle tautologie della LG nell'insieme delle tautologie della LC.
 +
* Introduzione del problema di tautologicità nella LG.
 +
* Lemma: l'insieme dei possibili valori di verità di una formula è composto da 1, 0 e i valori di verità delle variabili coinvolte nella formula.
 +
 +
''Oggi sono state distribuite le fotocopie del primo capitolo delle dispense.''
 +
 +
 +
=== Lezione di venerdì 12/10/2007 ===
 +
 +
* Definizione degli assiomi della LG e di formule deducibili (o dimostrabili).
 +
* Teorema di completezza per la LG (senza dimostrazione).
 +
* Definizione di assegnamenti equivalenti su n variabili (che si scrive <math>\mu\equiv_n\nu</math>).
 +
* Lemma: dati due assegnamenti <math>\mu</math> e <math>\nu</math> equivalenti sulle prime n variabili, per ogni formula <math>\alpha \left( x_1 , \ldots , x_n \right)</math> vale:
 +
<math>
 +
\begin{matrix}
 +
\mu\left(\alpha\right)=1 &\Leftrightarrow& \nu\left(\alpha\right)=1 \\
 +
\mu\left(\alpha\right)=\mu\left(x_i\right) &\Leftrightarrow& \nu\left(\alpha\right)=\nu\left(x_i\right) \\
 +
\mu\left(\alpha\right)=0 &\Leftrightarrow& \nu\left(\alpha\right)=0 \\
 +
\end{matrix}
 +
</math>
 +
* Corollario: il problema di tautologicità della LG è decidibile.
 +
 +
 +
=== Lezione di martedì 16/10/2007 ===
 +
 +
* Algoritmo per la risoluzione del problema di tautologicità.
 +
* Dimostrazione intuitiva del fatto che esiste sempre un assegnamento coerente con ogni catena di segni (purchè non siano tutti '=').
 +
* Relazione d'ordine <math>{\leq}_n</math> tra le classi di equivalenza degli assegnamenti nella LG.
 +
* Rappresentazione di <math>\mathcal{F}_n</math> (= insieme delle classi di equivalenza degli assegnamenti su n variabili nella LG) tramite diagrammi di Hasse.
 +
 +
 +
=== Lezione di venerdì 19/10/2007 ===
 +
 +
* Definizioni di: relazione (riflessiva, simmetrica, transitiva, antisimmetrica, di equivalenza, d'ordine), insieme parzialmente ordinato (=poset), insieme totalmente ordinato (=catena), elementi inconfrontabili, sottoposet, downset, foresta, elemento minimale, minimo, albero.
 +
* Lemma: per ogni n, la struttura <math>\left( \mathcal{F}_n , {\leq}_n \right)</math> è una foresta (dimostrazione lasciata per esercizio).
 +
 +
 +
=== Lezione di martedì 23/10/2007 ===
 +
 +
* Definizioni di downset di un insieme e sottoforesta.
 +
* Equivalenza semantica e sintattica delle formule (sia nella LC sia nella LG), definizione di 1-set di una formula <math>\alpha</math> nella LC (insieme associato <math>I_\alpha</math>) e nella LG (foresta associata <math>F_\alpha</math>), di classe di equivalenza di una formula.
 +
* Lemma: la foresta associata ad una formula n-aria è una sottoforesta di <math>\mathcal{F}_n</math>.
 +
* Lemma di sconnessione delle foreste: due formule sono equivalenti sse le foreste ad esse associate coincidono.
 +
* Definizione di foglie e radici di una foresta.
 +
* Fatto: <math>\left[\mu\right] \in \mathcal{F}_n</math> è una foglia sse <math>\mu\left(x_i\right)=1</math> per ogni i = 1,...,n .
 +
 +
 +
=== Lezione di venerdì 26/10/2007 ===
 +
 +
'''Forme normali disgiuntive (DNF)'''
 +
 +
* Definizioni (nella logica classica) di: letterale, clausola congiuntiva, mintermine, formula in DNF.
 +
* Definizioni (nella logica di Gödel) di: formula equivalente a un mintermine, clausola di Gödel.
 +
* Teorema:
 +
<math>
 +
\begin{matrix}
 +
F_{\alpha\vee\beta} &=& F_\alpha \cup F_\beta \\
 +
F_{\alpha\wedge\beta} &=& F_\alpha \cap F_\beta \\
 +
F_{\bot} &=& \emptyset \\
 +
F_{\top} &=& \mathcal{F}_n \\
 +
\end{matrix}
 +
</math>
 +
* Esercizio per casa: trovare <math>F_{\alpha\rightarrow\beta}</math> e <math>F_{\neg\alpha}</math>.
 +
* Osservazione: una foresta può sempre essere scritta come unione dei suoi rami massimali.
 +
* Osservazione 2: una foresta <math>F</math> può essere sintetizzata dalla formula <math>\alpha</math> (cioè <math>F_\alpha = F</math>) se <math>\alpha</math> è ottenibile come disgiunzione di formule che sintetizzano i rami massimali di <math>F</math>.
 +
* Definizione del connettivo <math>\triangleleft</math> (che si legge "minore di"):
 +
<math>\beta \triangleleft \alpha \equiv \left( \alpha \rightarrow \beta \right) \rightarrow \alpha</math>.
 +
* Definizione alternativa:
 +
<math>
 +
\mu\left(\beta \triangleleft \alpha\right) = \left\{
 +
\begin{matrix}
 +
1 & \mbox{ se } \mu\left(\beta\right) < \mu\left(\alpha\right) \mbox{ oppure } \mu\left(\beta\right) = \mu\left(\alpha\right) = 1 \\
 +
\mu\left(\alpha\right) & \mbox{altrimenti} \\
 +
\end{matrix} \right.
 +
</math>
 +
* Definizione di formula <math>\alpha_\mu</math> associata a <math>\left[\mu\right]</math>.
 +
* Lemma: il downset di <math>\left[\mu\right]</math> coincide con la foresta associata ad <math>\alpha_\mu</math>.
 +
 +
 +
=== Lezione di martedì 30/10/2007 ===
 +
 +
* Esempi di corrispondenza tra clausole di Gödel e rami di <math>\mathcal{F}_n</math>.
 +
* Lemma: una clausola risulta vera esattamente per gli assegnamenti nel downset del nodo corrispondente alla scelta di segni della clausola.
 +
* Lemma: data una foresta F qualsiasi, esiste sempre un n nei naturali tale che F si immerge in <math>\mathcal{F}_n</math> (cioè F è isomorfa a una foresta contenuta in <math>\mathcal{F}_n</math>).
 +
'''Sistemi Fuzzy''' (argomento facoltativo)
 +
* Introduzione ai sistemi fuzzy ([http://en.wikipedia.org/wiki/Fuzzy_control_system pagina di Wikipedia]).
 +
* Definizione di fuzzy set.
 +
* Formalizzazione delle regole fuzzy e  assiomi extralogici.
 +
* Esempi e considerazioni sugli insiemi fuzzy in relazione alle logiche polivalenti.
 +
 +
 +
=== Lezione di martedì 6/11/2007 ===
 +
 +
'''Seminario'''
 +
Paolo Amato, ST Microelectronics-M6. '''Logica Fuzzy e Applicazioni Industriali'''.
 +
 +
 +
=== Lezione di martedì 13/11/2007 ===
 +
 +
'''Semantica temporale della LG'''
 +
* Definizioni di assegnamento atomico o alle formule e di tautologia secondo la semantica temporale.
 +
* Semantica temporale dei connettivi.
 +
* Teorema di completezza per la semantica temporale (senza dimostrazione ma con un paio di esempi).
 +
* Relazione tra gli assegnamenti nella semantica temporale e le foreste <math>\mathcal{F}_n</math>.
 +
 +
''Oggi si è conclusa ufficialmente la parte sulla logica di Gödel con Marra, dalla prossima lezione comincerà la parte sulla logica di Łukasiewicz tenuta da Aguzzoli.''
 +
 +
 +
=== Lezione di venerdì 16/11/2007 ===
 +
 +
'''Introduzione alle logiche polivalenti basate su t-norme'''
 +
* Riassunto delle caratteristiche principali della LG e relazione con la LC.
 +
* Rappresentazione grafica della semantica dei connettivi della LG.
 +
* Correttezza del modus ponens fuzzy.
 +
* Definizione di t-norma e esempi di t-norme (tra cui la t-norma di Łukasiewicz).
 +
* Residuazione, residuo, condizione di esistenza del residuo.
 +
* Congiunzione, implicazione e negazione nella logica di Łukasiewicz.
 +
 +
 +
=== Lezione di martedì 20/11/2007 ===
 +
 +
* Grafico della negazione in funzione dello 0-set della t-norma.
 +
* Implicazione in Łukasiewicz: funzione algebrica e grafico.
 +
* Introduzione a BL (basic logic).
 +
* Gerarchia delle logiche: BL, LG, LŁ, LC, logica prodotto e relazioni tra esse.
 +
 +
 +
=== Lezione di venerdì 23/11/2007 ===
 +
 +
* Definizione di congiunzione/disgiunzione forte/debole.
 +
* Teorema: fissando una t-norma, vengono automaticamente definite una congiunzione debole e una disgiunzione debole.
 +
* Proprietà dell'implicazione:
 +
x -> x = 1
 +
1 -> x = x
 +
se x <= y allora x -> y = 1
 +
* Disgiunzione forte in Łukasiewicz, definizione di t-conorma.
 +
* Dimostrazione del fatto che <math>\left\{ \bigodot \lnot \right\}</math>, <math>\left\{ \oplus \lnot \right\}</math>, <math>\left\{ \rightarrow \lnot \right\}</math> sono tre possibili scelte di connettivi primitivi in Łukasiewicz.
 +
* Connettivi derivati: <math>\leftrightarrow</math>, <math>\vee</math>, <math>\wedge</math>.
 +
* Sintassi della logica di Łukasiewicz: alfabeto, formule, teorema di unica leggibilità.
 +
* Semantica [0,1]: assegnamento, assgnamento esteso, formula [0,1]-soddisfacibile, [0,1]-1-soddisfacibile, [0,1]-tautologia.
 +
* Proprietà della logica di Łukasiewicz:
 +
se <math>\varphi</math> è una [0,1]-tautologia, allora <math>\lnot \varphi</math> è [0,1]-insoddisfacibile
 +
se <math>\varphi</math> è [0,1]-soddisfacibile, allora <math>\lnot \varphi</math> non è una [0,1]-tautologia.
 +
 +
 +
=== Lezione di martedì 27/11/2007 ===
 +
 +
* Definizione di teoria e di conseguenza logica nella semantica [0,1].
 +
* Calcolo di Łukasiewicz (=sintassi): schemi di assiomi e regola di inferenza.
 +
* Definizione di prova e di prova da una teoria.
 +
* Enunciato del teorema di correttezza e completezza.
 +
* Teorema: per verificare la [0,1]-tautologia di un assioma basta verificare la [0,1]-tautologia di una sua istanza su variabili.
 +
* Dimostrazione di correttezza del modus ponens e di [0,1]-tautologicità degli assiomi.
 +
* Dimostrazione del teorema di correttezza.
 +
* Esempi di formule provabili.
 +
 +
 +
=== Lezione di martedì 4/12/2007 ===
 +
 +
* Considerazioni sul significato degli assiomi del calcolo di Łukasiewicz.
 +
* Schema di assiomi per il calcolo per la LC.
 +
* Definizione di funzione termine.
 +
* Corrispondenza tra le funzioni termine costanti 1 e le [0,1]-tautologie.
 +
* Completezza funzionale della LC (che in genere non vale nelle logiche polivalenti).
 +
* Funzioni di McNaughton: definizione e esempi.
 +
* Teorema di rappresentazione di Mc Naughton e dimostrazione di un lato della doppia implicazione (funzioni termine -> funzioni Mc Naughton).
 +
 +
 +
=== Lezione di martedì 11/12/2007 ===
 +
 +
* Fine della dimostrazione della volta scorsa (funzioni termine -> funzioni Mc Naughton).
 +
* Lemma di Rose-Rosser (con dimostrazione).
 +
 +
 +
=== Lezione di venerdì 14/12/2007 ===
 +
 +
* Sequenze di Farey.
 +
* Teorema di Farey-Cauchy.
 +
* Cappelli di Schauder.
 +
* Lemma: I cappelli di Schauder sono funzioni di Mc Naughton (con dimostrazione).
 +
* Metodo iterativo per la costruzione di sequenze di Farey (e visione geometrica dell'algoritmo coi cappelli di Schauder).
 +
 +
 +
=== Lezione di martedì 18/12/2007 ===
 +
 +
* Dimostrazione del secondo lato del teorema di McNaughton (funzioni Mc Naughton -> funzioni termine) nel caso particolare di una sola variabile.
 +
* Accenno al caso con 2 variabili.
 +
 +
 +
=== Lezione di venerdì 21/12/2007 ===
 +
 +
* Equivalenza logica sintattica e semantica tra formule.
 +
* La relazione di equivalenza logica sintattica è una relazione di congruenza (dimostrazione).
 +
* Definizione di MV-algebra ed esempi di MV-algebre.
 +
* Algebra di Lindenbaum.
 +
* L'algebra di Lindenbaum è una MV-algebra (dimostrazione).
 +
 +
 +
=== Lezione di martedì 8/1/2008 ===
 +
 +
* Fine della dimostrazione del fatto che l'algebra di Lindenbaum è una MV-algebra.
 +
* Definizioni di: assegnamento, assegnamento esteso, equazioni valide e funzioni termine in una MV-algebra.
 +
* Teorema di completezza algebrica di Chang (senza dimostrazione).
 +
* Teorema di completezza per la logica di Łukasiewicz.

Versione attuale delle 08:36, 21 set 2010

News

ultima lezione: venerdì 11 gennaio

Appelli

Su appuntamento.

Informazioni generali

Sito del corso

logicafuzzy.dsi.unimi.it

Docenti

Vincenzo Marra
Stefano Aguzzoli

Corsi di laurea

Complementare per i corsi di laurea triennale in Informatica, Informatica per le Telecomunicazioni e Comunicazione Digitale e per il corso di laurea magistrale in Informatica.

Programma

  • Prima Parte (Marra)
Introduzione alla logica fuzzy e alle sue applicazioni.
Logica proposizionale booleana.
Norme triangolari e relative logiche fuzzy.
Introduzione alla logica di Gödel.
Semantica della logica di Gödel.
Completezza della logica di Gödel.
Una semantica alternativa per la logica di Gödel.
Logica di Gödel e logica booleana a confronto.
  • Seconda Parte (Aguzzoli)
Introduzione alla logica di Łukasiewicz.
Logica di Łukasiewicz e logica di Gödel a confronto.
Semantica della logica di Łukasiewicz: le MV-algebre di Chang.
Completezza della logica di Łukasiewicz.
Teorema di rappresentazione di McNaughton.
Complessità computazionale dei problemi di soddisfacibilità e tautologicità della logica di Łukasiewicz.
Un approccio generale alle gerarchie di logiche fuzzy: cenni a BL e MTL.

Seminari

  • Nell'anno accademico 2007-2008 si prevedono i seminari seguenti:
Paolo Amato, ST Microelectronics. Titolo da stabilirsi. Data da stabilirsi.
Matteo Bianchi, Università di Milano. Estensioni predicative delle logiche fuzzy. Data da stabilirsi.
Simone Bova, Università di Siena. Introduzione alla Basic Fuzzy Logic di Hájek. Data da stabilirsi.

Modalità d'esame

L'esame consiste in un colloquio con i docenti sul programma del corso.

Gli studenti che ne facciano richiesta possono anche concordare con i docenti la redazione di una tesina o lo sviluppo di un progetto in sostituzione di parti del programma.

Alcuni esempi di tesine: relazione su un articolo di ricerca; rassegna della letteratura scientifica su un argomento di ricerca.

Alcuni esempi di progetti: implementazione (in C, Java, Prolog, etc.) di algoritmi inerenti al programma del corso; sviluppo di software di supporto alla ricerca nel campo della logica fuzzy.

Prerequisiti al corso

Nessuno.

Orari e luogo delle lezioni

  • Martedì 13.30-15.30 auletta 5 (Comelico)
  • Venerdì 13.30-15.30 auletta 5 (Comelico)

Orario di ricevimento studenti

  • Marra: su appuntamento.
  • Aguzzoli: mercoledì dalle 15.00 alle 16.00 o su appuntamento, stanza S204 via Comelico 39.

Materiale didattico

Non ci sono testi che coprano interamente gli argomenti trattati, ma il contenuto delle lezioni è sufficiente per sostenere l'esame.

Testi ausiliari consigliati

R. L. O. Cignoli, I. M. L. D'Ottaviano e D. Mundici, Algebraic Foundations of Many-Valued Reasoning, Kluwer, 1999.
P. Hájek, Metamathematics of Fuzzy Logic, Kluwer, 1998.
S. Gottwald, A Treatise on Many-Valued Logics, King's College Publications, Research Studies Press, 2001.

Dispense

 Durante le lezioni verrà distribuita una versione preliminare delle dispense del corso.

Diario del corso

Lezione di martedì 2/10/2007

  • Definizione di logica fuzzy in senso stretto e in senso ampio.
  • Concetti di funzione di appartenenza e di insiemi fuzzy.
  • Richiamo di logica proposizionale classica: definizioni di proposizione atomica, proposizione composta, alfabeto, stringa, formula.


Lezione di venerdì 5/10/2007

Semantica della logica proposizionale classica

  • Assegnamento alle variabili e assegnamento alle formule.
  • Definizioni di tautologia, contraddizione e formula soddisfacibile.
  • Esempi di tautologie: prelinearità, principio del terzo escluso, ex falso quodlibet, leggi di de Morgan.

Teoria della dimostrazione (sintassi)

  • Assiomi della LPC.
  • Definizione di dimostrabilità e derivabilità per modus ponens.
  • Teorema di completezza della LPC.


Lezione di martedì 9/10/2007

Logica di Gödel

  • Definizione di assegnamento alle variabili e alle formule nella LG (e variante di Zadeh).
  • Analisi di alcune tautologie della LC che cadono nella LG (legge della doppia negazione, principio del terzo escluso) o restano tautologie (ex falso quodlibet, prelinearità).
  • Inclusione stretta dell'insieme delle tautologie della LG nell'insieme delle tautologie della LC.
  • Introduzione del problema di tautologicità nella LG.
  • Lemma: l'insieme dei possibili valori di verità di una formula è composto da 1, 0 e i valori di verità delle variabili coinvolte nella formula.

Oggi sono state distribuite le fotocopie del primo capitolo delle dispense.


Lezione di venerdì 12/10/2007

  • Definizione degli assiomi della LG e di formule deducibili (o dimostrabili).
  • Teorema di completezza per la LG (senza dimostrazione).
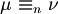  • Definizione di assegnamenti equivalenti su n variabili (che si scrive \mu \equiv _{n}\nu ).
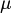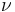  • Lemma: dati due assegnamenti \mu e \nu equivalenti sulle prime n variabili, per ogni formula 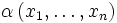\alpha \left(x_{1},\ldots ,x_{n}\right) vale:
{\begin{matrix}\mu \left(\alpha \right)=1&\Leftrightarrow &\nu \left(\alpha \right)=1\\\mu \left(\alpha \right)=\mu \left(x_{i}\right)&\Leftrightarrow &\nu \left(\alpha \right)=\nu \left(x_{i}\right)\\\mu \left(\alpha \right)=0&\Leftrightarrow &\nu \left(\alpha \right)=0\\\end{matrix}}
  • Corollario: il problema di tautologicità della LG è decidibile.


Lezione di martedì 16/10/2007

  • Algoritmo per la risoluzione del problema di tautologicità.
  • Dimostrazione intuitiva del fatto che esiste sempre un assegnamento coerente con ogni catena di segni (purchè non siano tutti '=').
  • Relazione d'ordine 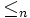{\leq }_{n} tra le classi di equivalenza degli assegnamenti nella LG.
  • Rappresentazione di 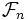{\mathcal {F}}_{n} (= insieme delle classi di equivalenza degli assegnamenti su n variabili nella LG) tramite diagrammi di Hasse.


Lezione di venerdì 19/10/2007

  • Definizioni di: relazione (riflessiva, simmetrica, transitiva, antisimmetrica, di equivalenza, d'ordine), insieme parzialmente ordinato (=poset), insieme totalmente ordinato (=catena), elementi inconfrontabili, sottoposet, downset, foresta, elemento minimale, minimo, albero.
  • Lemma: per ogni n, la struttura 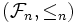\left({\mathcal {F}}_{n},{\leq }_{n}\right) è una foresta (dimostrazione lasciata per esercizio).


Lezione di martedì 23/10/2007

  • Definizioni di downset di un insieme e sottoforesta.
  • Equivalenza semantica e sintattica delle formule (sia nella LC sia nella LG), definizione di 1-set di una formula 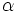\alpha nella LC (insieme associato 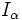I_{\alpha }) e nella LG (foresta associata 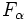F_{\alpha }), di classe di equivalenza di una formula.
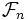  • Lemma: la foresta associata ad una formula n-aria è una sottoforesta di {\mathcal {F}}_{n}.
  • Lemma di sconnessione delle foreste: due formule sono equivalenti sse le foreste ad esse associate coincidono.
  • Definizione di foglie e radici di una foresta.
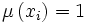  • Fatto: \left[\mu \right]\in {\mathcal {F}}_{n} è una foglia sse \mu \left(x_{i}\right)=1 per ogni i = 1,...,n .


Lezione di venerdì 26/10/2007

Forme normali disgiuntive (DNF)

  • Definizioni (nella logica classica) di: letterale, clausola congiuntiva, mintermine, formula in DNF.
  • Definizioni (nella logica di Gödel) di: formula equivalente a un mintermine, clausola di Gödel.
  • Teorema:
{\begin{matrix}F_{{\alpha \vee \beta }}&=&F_{\alpha }\cup F_{\beta }\\F_{{\alpha \wedge \beta }}&=&F_{\alpha }\cap F_{\beta }\\F_{{\bot }}&=&\emptyset \\F_{{\top }}&=&{\mathcal  {F}}_{n}\\\end{matrix}}
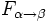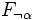  • Esercizio per casa: trovare F_{{\alpha \rightarrow \beta }} e F_{{\neg \alpha }}.
  • Osservazione: una foresta può sempre essere scritta come unione dei suoi rami massimali.
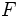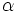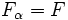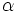  • Osservazione 2: una foresta F può essere sintetizzata dalla formula \alpha (cioè F_{\alpha }=F) se \alpha è ottenibile come disgiunzione di formule che sintetizzano i rami massimali di F.
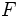  • Definizione del connettivo 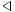\triangleleft (che si legge "minore di"):
\beta \triangleleft \alpha \equiv \left(\alpha \rightarrow \beta \right)\rightarrow \alpha .
  • Definizione alternativa:
\mu \left(\beta \triangleleft \alpha \right)=\left\{{\begin{matrix}1&{\mbox{ se }}\mu \left(\beta \right)<\mu \left(\alpha \right){\mbox{ oppure }}\mu \left(\beta \right)=\mu \left(\alpha \right)=1\\\mu \left(\alpha \right)&{\mbox{altrimenti}}\\\end{matrix}}\right.
  • Definizione di formula 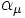\alpha _{\mu } associata a \left[\mu \right].
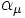  • Lemma: il downset di \left[\mu \right] coincide con la foresta associata ad \alpha _{\mu }.


Lezione di martedì 30/10/2007

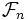  • Esempi di corrispondenza tra clausole di Gödel e rami di {\mathcal {F}}_{n}.
  • Lemma: una clausola risulta vera esattamente per gli assegnamenti nel downset del nodo corrispondente alla scelta di segni della clausola.
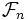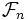  • Lemma: data una foresta F qualsiasi, esiste sempre un n nei naturali tale che F si immerge in {\mathcal {F}}_{n} (cioè F è isomorfa a una foresta contenuta in {\mathcal {F}}_{n}).

Sistemi Fuzzy (argomento facoltativo)

  • Introduzione ai sistemi fuzzy (pagina di Wikipedia).
  • Definizione di fuzzy set.
  • Formalizzazione delle regole fuzzy e assiomi extralogici.
  • Esempi e considerazioni sugli insiemi fuzzy in relazione alle logiche polivalenti.


Lezione di martedì 6/11/2007

Seminario 

Paolo Amato, ST Microelectronics-M6. Logica Fuzzy e Applicazioni Industriali.


Lezione di martedì 13/11/2007

Semantica temporale della LG

  • Definizioni di assegnamento atomico o alle formule e di tautologia secondo la semantica temporale.
  • Semantica temporale dei connettivi.
  • Teorema di completezza per la semantica temporale (senza dimostrazione ma con un paio di esempi).
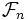  • Relazione tra gli assegnamenti nella semantica temporale e le foreste {\mathcal {F}}_{n}.

Oggi si è conclusa ufficialmente la parte sulla logica di Gödel con Marra, dalla prossima lezione comincerà la parte sulla logica di Łukasiewicz tenuta da Aguzzoli.


Lezione di venerdì 16/11/2007

Introduzione alle logiche polivalenti basate su t-norme

  • Riassunto delle caratteristiche principali della LG e relazione con la LC.
  • Rappresentazione grafica della semantica dei connettivi della LG.
  • Correttezza del modus ponens fuzzy.
  • Definizione di t-norma e esempi di t-norme (tra cui la t-norma di Łukasiewicz).
  • Residuazione, residuo, condizione di esistenza del residuo.
  • Congiunzione, implicazione e negazione nella logica di Łukasiewicz.


Lezione di martedì 20/11/2007

  • Grafico della negazione in funzione dello 0-set della t-norma.
  • Implicazione in Łukasiewicz: funzione algebrica e grafico.
  • Introduzione a BL (basic logic).
  • Gerarchia delle logiche: BL, LG, LŁ, LC, logica prodotto e relazioni tra esse.


Lezione di venerdì 23/11/2007

  • Definizione di congiunzione/disgiunzione forte/debole.
  • Teorema: fissando una t-norma, vengono automaticamente definite una congiunzione debole e una disgiunzione debole.
  • Proprietà dell'implicazione:
x -> x = 1
1 -> x = x
se x <= y allora x -> y = 1
  • Disgiunzione forte in Łukasiewicz, definizione di t-conorma.
  • Dimostrazione del fatto che 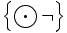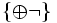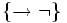\left\{\bigodot \lnot \right\}, \left\{\oplus \lnot \right\}, \left\{\rightarrow \lnot \right\} sono tre possibili scelte di connettivi primitivi in Łukasiewicz.
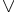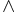  • Connettivi derivati: \leftrightarrow , \vee , \wedge .
  • Sintassi della logica di Łukasiewicz: alfabeto, formule, teorema di unica leggibilità.
  • Semantica [0,1]: assegnamento, assgnamento esteso, formula [0,1]-soddisfacibile, [0,1]-1-soddisfacibile, [0,1]-tautologia.
  • Proprietà della logica di Łukasiewicz:
se \varphi  è una [0,1]-tautologia, allora \lnot \varphi  è [0,1]-insoddisfacibile
se \varphi  è [0,1]-soddisfacibile, allora \lnot \varphi  non è una [0,1]-tautologia.


Lezione di martedì 27/11/2007

  • Definizione di teoria e di conseguenza logica nella semantica [0,1].
  • Calcolo di Łukasiewicz (=sintassi): schemi di assiomi e regola di inferenza.
  • Definizione di prova e di prova da una teoria.
  • Enunciato del teorema di correttezza e completezza.
  • Teorema: per verificare la [0,1]-tautologia di un assioma basta verificare la [0,1]-tautologia di una sua istanza su variabili.
  • Dimostrazione di correttezza del modus ponens e di [0,1]-tautologicità degli assiomi.
  • Dimostrazione del teorema di correttezza.
  • Esempi di formule provabili.


Lezione di martedì 4/12/2007

  • Considerazioni sul significato degli assiomi del calcolo di Łukasiewicz.
  • Schema di assiomi per il calcolo per la LC.
  • Definizione di funzione termine.
  • Corrispondenza tra le funzioni termine costanti 1 e le [0,1]-tautologie.
  • Completezza funzionale della LC (che in genere non vale nelle logiche polivalenti).
  • Funzioni di McNaughton: definizione e esempi.
  • Teorema di rappresentazione di Mc Naughton e dimostrazione di un lato della doppia implicazione (funzioni termine -> funzioni Mc Naughton).


Lezione di martedì 11/12/2007

  • Fine della dimostrazione della volta scorsa (funzioni termine -> funzioni Mc Naughton).
  • Lemma di Rose-Rosser (con dimostrazione).


Lezione di venerdì 14/12/2007

  • Sequenze di Farey.
  • Teorema di Farey-Cauchy.
  • Cappelli di Schauder.
  • Lemma: I cappelli di Schauder sono funzioni di Mc Naughton (con dimostrazione).
  • Metodo iterativo per la costruzione di sequenze di Farey (e visione geometrica dell'algoritmo coi cappelli di Schauder).


Lezione di martedì 18/12/2007

  • Dimostrazione del secondo lato del teorema di McNaughton (funzioni Mc Naughton -> funzioni termine) nel caso particolare di una sola variabile.
  • Accenno al caso con 2 variabili.


Lezione di venerdì 21/12/2007

  • Equivalenza logica sintattica e semantica tra formule.
  • La relazione di equivalenza logica sintattica è una relazione di congruenza (dimostrazione).
  • Definizione di MV-algebra ed esempi di MV-algebre.
  • Algebra di Lindenbaum.
  • L'algebra di Lindenbaum è una MV-algebra (dimostrazione).


Lezione di martedì 8/1/2008

  • Fine della dimostrazione del fatto che l'algebra di Lindenbaum è una MV-algebra.
  • Definizioni di: assegnamento, assegnamento esteso, equazioni valide e funzioni termine in una MV-algebra.
  • Teorema di completezza algebrica di Chang (senza dimostrazione).
  • Teorema di completezza per la logica di Łukasiewicz.
Estratto da "https://wiki.dsy.it/index.php?title=Logica_fuzzy/2007-2008&oldid=20534"