Differenze tra le versioni di "Teoria dei grafi"

Da WikiDsy.
m (→‎V 22 Ottobre)
 
(12 versioni intermedie di 3 utenti non mostrate)
Riga 1: Riga 1:
 +
[http://dl.dropbox.com/u/5745163/dantona-paper.zip Paper dati dal prof. a lezione il 13 gennaio]
 +
 
{{introduzione}}
 
{{introduzione}}
 
== Informazioni generali ==
 
== Informazioni generali ==
Riga 61: Riga 63:
  
 
===G 28 Ottobre===
 
===G 28 Ottobre===
 +
*Combinazioni tra ''n'' palline indistinguibili in ''x'' scatole distinguibili come numero di funzioni monotone tra due catene lunghe ''n'' e ''x''
 +
**Definizione ricorsiva di questa ''f(n, x)''
 +
**Valore della sommatoria degli interi da 1 a ''i'' (con dimostrazione di Gauss)
 +
*Definizione non ricorsiva di questa ''f(n, x)'' come <math>\frac{<x>_n}{x!}</math>
 +
**Definizione di "x crescente n" come <math>x\cdot(x+1)\cdot(x+2) ... \cdot(x+n-1)</math>
  
 
===V 29 Ottobre===
 
===V 29 Ottobre===
 +
 +
===V 05 Novembre===
 +
*Audio della lezione: [http://dl.dropbox.com/u/1131549/TeoriaDeiGrafi/TeoriaDeiGrafi_20101105.mp3 TeoriaDeiGrafi_20101105.mp3]
 +
*Appunti della lezione: [http://dl.dropbox.com/u/1131549/TeoriaDeiGrafi/TeoriaDeiGrafi_20101105.rar TeoriaDeiGrafi_20101105.rar]
 +
 +
===L 08 Novembre===
 +
*Audio della lezione:
 +
**Parte 1 : [http://dl.dropbox.com/u/1131549/TeoriaDeiGrafi/TeoriaDeiGrafi_20101108_1.mp3 TeoriaDeiGrafi_20101108_1.mp3]
 +
**Parte 2 : [http://dl.dropbox.com/u/1131549/TeoriaDeiGrafi/TeoriaDeiGrafi_20101108_2.mp3 TeoriaDeiGrafi_20101108_2.mp3]
 +
*Appunti della lezione : [http://www.megaupload.com/?d=ZM6OLNGW Teoria_dei_grafi_20101108.rar]
 +
 +
===G 11 Novembre===
 +
*Appunti della lezione : [http://www.megaupload.com/?d=63S0XXBC Teoria_dei_grafi_20101111.rar]
 +
 +
===L 15 Novembre===
 +
*Appunti della lezione : [http://www.megaupload.com/?d=G2VACJV0 Teoria_dei_grafi_20101115.rar]
 +
 +
...
 +
 +
===G 13 Gennaio===
 +
* <big><big>[http://dl.dropbox.com/u/5745163/dantona-paper.zip Paper dati dal prof. a lezione]</big></big>
  
 
== Esercizi assegnati ==
 
== Esercizi assegnati ==
Riga 68: Riga 96:
  
 
===L 18 Ottobre===
 
===L 18 Ottobre===
 +
*Trovare una procedura efficiente per il calcolo del coefficiente binomiale
 +
*Scrivere lo sviluppo di Mc-Laurin della funzione <math>e^{e^x-1}</math>
 
*Dimostrare che l' insieme delle parole binarie (compresa la parola vuota) è enumerabile
 
*Dimostrare che l' insieme delle parole binarie (compresa la parola vuota) è enumerabile
  
Riga 84: Riga 114:
  
 
===G 28 Ottobre===
 
===G 28 Ottobre===
 +
*Dimostrare che <math>\frac{n\cdot(n+1)\cdot(n+2)}{2\cdot3}\in Z</math>
 +
*Calcolare quante sono le associazioni monotòne da una catena di ''n'' elementi a un albero binario completo di ''x'' elementi <small>(era un esercizio o qualcosa che vedremo nelle prossime lezioni?)</small>
  
 
===V 29 Ottobre===
 
===V 29 Ottobre===
 +
  
 
== Turni ==
 
== Turni ==

Versione attuale delle 17:23, 16 gen 2011

Paper dati dal prof. a lezione il 13 gennaio

Disambigua compass.PNG
 Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata.

Informazioni generali

Teoria dei grafi è un insegnamento complementare dei Corsi di Laurea del DSI/DICo.

Docente

Ottavio Mario D'Antona

Orari delle lezioni

  • Lunedì 17.30 - 19.30 (aula alfa)
  • Giovedì 17.30 - 19.30 (aula alfa)
  • Venerdì 16.30 - 18.30 (auletta 5)

Sito del corso

http://homes.dico.unimi.it/~dantona/tg/ (non aggiornato)

Materiale didattico

  • Ottavio Mario D'Antona - "Introduzione alla matematica discreta" (ed. Apogeo)

Diario del Corso

V 15 Ottobre

L 18 Ottobre

  • ( Dimostrazione che l' insieme dei numeri reali non è enumerabile )
  • Definizione di partizione di un insieme
  • Relazione tra funzioni suriettive e partizioni

G 21 Ottobre

  • Numeri di Stirling
    • Numeri di Stirling e triangolo di Tartaglia
    • Equazione S(n,k) = S(n-1,k-1) + kS(n-1,k)
  • Numeri di E.T. Bell
  • Concetto di "fattorizzazione" di una funzione tramite insieme ghost
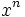  • x^{n} come sommatoria di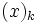 (x)_{k}

V 22 Ottobre

  • Funzione Generatrice (esponenziale e ordinaria)
    • dei numeri di Bell
    • dei numeri di Fibonacci
  • Grafi e matrici come rappresentazione delle relazioni
  • Relazioni di equivalenza
    • Matrice a blocchi
  • Partial order relations
    • Nella teoria dei numeri: rel. di divisibilità
    • Nelle'algebra di Boole: rel. di raffinamento
  • Diagramma di Hasse
  • Greatest Lower Bound e Least Upper Bounds
  • Reticoli

L 25 Ottobre

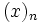  • (x)_{n} come sommatoria di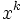 x^{k}
  • Insieme parzialmento ordinato dotato di rango: rota-poset
  • Funzione di Möbius
  • Catene e prodotto di catene
  • La relazione "contiene tutti i punti di" tra le facce n-dimensionali di un solido
    • I complessi simpliciali, il triangolo di Tartaglia e l'algebra di Boole
  • Reticolo geometrico

G 28 Ottobre

  • Combinazioni tra n palline indistinguibili in x scatole distinguibili come numero di funzioni monotone tra due catene lunghe n e x
    • Definizione ricorsiva di questa f(n, x)
    • Valore della sommatoria degli interi da 1 a i (con dimostrazione di Gauss)
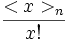
  • Definizione non ricorsiva di questa f(n, x) come {\frac {<x>_{n}}{x!}}
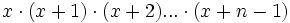
    • Definizione di "x crescente n" come x\cdot (x+1)\cdot (x+2)...\cdot (x+n-1)

V 29 Ottobre

V 05 Novembre

L 08 Novembre

G 11 Novembre

L 15 Novembre

...

G 13 Gennaio

Esercizi assegnati

V 15 Ottobre

L 18 Ottobre

  • Trovare una procedura efficiente per il calcolo del coefficiente binomiale
  • Scrivere lo sviluppo di Mc-Laurin della funzione e^{{e^{x}-1}}
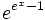
  • Dimostrare che l' insieme delle parole binarie (compresa la parola vuota) è enumerabile

G 21 Ottobre

V 22 Ottobre

  • Calcolare la funzione generatrice ordinaria dei numeri di "Tribonacci"
  • Calcolare in quanti modi è possibile disporre dei rettangoli 1x2 per riempire un rettangolo 2xn
  • Determinare se la relazione "ha più blocchi?" applicata alle partizioni di un insieme forma un reticolo
  • Scrivere un algoritmo efficiente per determinare, data una matrice di adiacenza, se la corrispondente relazione è di equivalenza

L 25 Ottobre

  • Dimostrare che la funzione di Möbius in un'algebra di Boole vale sempre +1 o -1
  • Trovare per gli n-cubi il numero di facce k-dimensionali (come fatto per i simplessi e Tartaglia)
  • Dimostrare che presi m interi positivi consecutivi (n ... n+m-1) il loro prodotto sarà divisibile per m!

G 28 Ottobre

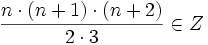
  • Dimostrare che {\frac {n\cdot (n+1)\cdot (n+2)}{2\cdot 3}}\in Z
  • Calcolare quante sono le associazioni monotòne da una catena di n elementi a un albero binario completo di x elementi (era un esercizio o qualcosa che vedremo nelle prossime lezioni?)

V 29 Ottobre

Turni

A.A. passati

Informazioni

Giudizio sul corso

I giudizi di seguito espressi sono il parere personale degli studenti,
e potrebbero non rispecchiare il parere medio dei frequentanti.
Non vi è comunque alcun intento di mettere alla gogna i docenti del corso!
Interesse della materia (da 1 a 5 - aiuto)
____________________
Difficoltà del corso (da 1 a 5 - aiuto)
____________________
Difficoltà del corso per non frequentanti (da 1 a 5 - aiuto)
____________________
Ore di studio richieste (da 1 a 5 - aiuto)
____________________
Estratto da "https://wiki.dsy.it/index.php?title=Teoria_dei_grafi&oldid=20873"