Differenze tra le versioni di "Architettura degli elaboratori Turno 3/2005-2006"
(→Lezione Giovedì 16 Marzo 2006) |
(→Lezione Giovedì 16 Marzo 2006) |
||
| Riga 301: | Riga 301: | ||
**Esempio con grafico di Venn | **Esempio con grafico di Venn | ||
| + | |||
| + | *Metodo per ottenere in forma canonica una funzione Booleana a partire dalla tabella di verità | ||
| + | **Esembio con tabella Multiplexer | ||
Versione delle 13:43, 27 mar 2006
Indice
News
GIOVEDI' 23 MARZO LEZIONE ANNULLATA
Anni precedenti
Informazioni generali
Docenti
Prof. D'Antona / Prof. Marra per il laboratorio.
Corsi di laurea
Modalità d'esame
Orale + Progetto
dal sito ufficiale: L'esame ha cadenza mensile, tendenzialmente di lunedì. Le date degli appelli sono pubblicate sul sito del D.I.Co. Il voto è determinato da due prove. Una è un'interrogazione tradizionale sugli argomenti trattati a lezione. La seconda consiste nella stesura di una porzione di programma in linguaggio Assembly MIPS (si vedano le due sezioni precedenti). Le due prove possono essere sostenute indipendentemente, purché a non più di 12 mesi l’una dall’altra, pena la necessità di ripetere la prova già sostenuta. Il voto per entrambe le prove è in trentesimi. Il voto finale, che potrà essere registrato solo dopo aver sostenuto con successo entrambe le prove, è ottenuto per media pesata dai due voti parziali. Il peso del progetto in Assembly è di un terzo del totale. Il tema del progetto è pubblicato su questa pagina tre volte l’anno, all’inizio dei quadrimestri gennaio-aprile, maggio-luglio, settembre-dicembre. Il candidato può consegnare in qualunque momento per posta elettronica all’indirizzo marra@dico.unimi.it l’elaborato relativo al tema d’esame corrente. Per poter registrare il voto finale in un dato appello, tuttavia, occorre consegnare il progetto una settimana prima dell’appello in questione, per dare il tempo ai docenti di valutare l’elaborato; le scadenze precise relative agli appelli correnti sono riportate nel tema d’esame. L’elaborato deve consistere di un solo file di testo contenente il sorgente Assembly, eventualmente corredato da un secondo file contenente la documentazione, in formato testo, Adobe PDF, o Rich Text Format.
Orari e luogo delle lezioni
| Martedì | Giovedì |
|---|---|
| 18:30-21:30 Aula 200 (via Golgi) | 18:30-21:30 Aula 200 (via Golgi) |
Orario di ricevimento studenti
Lunedì 12.00 - 14.00
Informazioni specifiche
Sito del corso
Forum del corso, e affini
Materiale Didattico
Programma del corso
Non ancora disponibile
TESTI
Testo di riferimento
- STRUCTURED COMPUTER ORGANIZATION 5 edizione autore Tanenbaum
la versione italiana del libro è in stampa in questi giorni
Altri testi Consigliati
- D.A. Patterson, J.L. Hennessy, Struttura, organizzazione e progetto dei calcolatori: interdipendenza tra hardware e software, Jackson libri, Milano, 1999 (seconda edizione).
- Per le reti di calcolatori: D. Comer, Internet e reti di calcolatori, Addison Wesley-Pearson Italia, Milano, 2003 (terza edizione).
- Il testo: O. D'Antona, E. Damiani, Ambienti esecutivi e di sviluppo dei linguaggi di programmazione, Addison Wesley-Masson, Milano, 1992, è una semplice introduzione preliminare agli argomenti del corso.
Altro materiale consigliato
Video delle lezioni
Le Lezioni saranno registrate durante il semestre e rese fruibili sul sito Virtual Classroom
NB. è necessario un account SILAB per accedere al sito
NB2 le lezioni dovrebbero essere online 7/10 giorni dopo la loro registrazione
Appunti
Appunti del corso a cura di Paolo Pavan:
MIPS
Convenzioni MIPS per il passaggio dei parametri discusse a lezione
Altro materiale in Internet
- Un utile ambiente di sviluppo gratuito (SO Windows), detto MIPSter, espressamente pensato per il simulatore SPIM (e l’assembly MIPS) è scaricabile da qui
- A questo indirizzo si trovano le pagine ufficiali su MIPSter
- Un versione dello SPIM per MacOS si trova a questoindirizzo, a cura di Daniel Franke
- Un buon editor gratuito è ConTEXT, reperibile a questo indirizzo. È prevista una modalità di evidenziazione della sintassi orientata all’assembly MIPS.
- Multipiattaforma trovate jEdit (in java), con parziale supporto alla sintassi MIPS
Esami passati, tesine, compiti ..
Diario del corso
Lezione Giovedì 9 Marzo 2006
- Introduzione al corso
si consigliano gli appunti reperibili dal sito ufficiale del corso a questo link
Lezione Martedì 14 Marzo 2006
- Ripasso lezione precedente
- Funzioni booleane (le funzioni booleane sono funzioni che ricevono in ingresso una nupla di 0,1 e restituiscono un BIT 0,1)
- I Mintermini(il mintermine è una funzione booleane che assume il valore 1 in corrispondenza di un unica configurazione di ingressi)
- Rapresentazione tramite diagramma di Venn di funzioni booleane
- Analogie fra funzioni Booleane e calcolo proposizionale (Una proposizione cioè una 'frase' da cui analogamente alle funzioni booleane ci si può aspettare 2 soli risultati Vero o Falso)
- la congiunzione logica
- la disgiunzione logica
- la negazione logica
- Accenni storici a Kurt Goedel e la Logica Polivalente
- Le Analogie con i circuiti
- Le porte Logiche ( logical Gate)
- cenni storici su Vanner Bush (padre dei calcolatori anologici), e su Claude Shannon (suo alievo che formalizzò la corrispondenza fra calcolo proposizionale e Circuiti)
- Riassunto Altre prinicpali propietà Algebra Booleana(elemento neutro delle operazioni , distributiva , assorbimento ....)
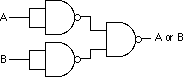
- AND
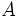 |
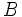 |
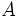 ∧ ∧ 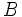
|
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
OR
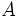 |
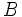 |
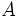 ∨ ∨ 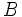
|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
NOT
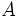 |
¬ 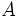
|
| F | T |
| T | F |
funzionalmente completi (sono cioè sufficenti ad esprimere una qualsiasi funzioni booleana
- NOT e AND/ NOT e OR sarebbero già sufficenti a esprimere qualsiasi espressione booleana (Dimostrazione usando De Morgan)
- La porta NAND da sola è sufficente ad esprimere qualsiasi funzione booleana
Sapendo che a NAND b = NOT( a AND b ) possiamo dimostrare che:
La funzione NOT a è esprimibile come a NAND a
NOT a = NOT( a AND a ) [ per idempotenza a AND a = a ]
NOT( a AND a ) = a NAND a [ per la definizione sopra ]
La funzione a AND b è esprimibile come ( a NAND b ) NAND ( a NAND b )
a AND b = NOT( NOT( a AND b ) ) [ per idempotenza NOT( NOT a ) = a ]
NOT( NOT( a AND b ) ) = NOT( a NAND b ) [ per la definizione sopra ]
NOT( a NAND b ) = ( a NAND b ) NAND ( a NAND b ) [ per la definizione di NOT utilizzando un NAND ]
La funzione a OR b è esprimibile come ( a NAND a ) NAND ( b NAND b )
a OR b = NOT( NOT( a ) ) OR NOT( NOT( b ) ) [ per idempotenza NOT( NOT a ) = a ]
NOT( NOT( a ) ) OR NOT( NOT( b ) ) = NOT( NOT( a ) AND NOT( b ) ) [ legge di De Morgan ]
NOT( NOT( a ) AND NOT( b ) ) = NOT( a ) NAND NOT( b ) [ per la definizione sopra ]
NOT( a ) NAND NOT( b ) = ( a NAND a ) NAND ( b NAND b ) [ per la definizione di NOT utilizzando un NAND ]
- Rappresentazione grafica dei circuiti
- Il Multiplexer e la sua rappresentazione
- esempio del loro uso combinato per la condivisione di una linea telefonica
DA FARE / DA PENSARE:
1)abbiamo visto che usando solo AND e OR non riusciamo ad esprimere tutte le possibili funzioni booleane, Quali e Quante funzioni riusciamo ad esprimere?
Lezione Giovedì 16 Marzo 2006
- tabella riassuntiva Connettori
| Insieme Connettori | Funzionalmente completo | Minimale | Minimo |
| AND,OR,NOT | SI | NO | NO |
| AND,NOT | SI | SI | NO |
| OR,NOT | SI | SI | NO |
| NAND | SI | SI | SI |
- ripasso Multiplexer (o selettore)
- Multiplexer con + di 2 ingressi
- Visto circuito Multiplexer a 3 Ingressi
- La formula per determinare il numero di variabili necessarie in un Multiplexer ad n ingressi (ceiling di Logaritmo in base 2 di n)
- il ceiling ed il flor di un numero reale
- Tabella di verità di un decoder 2 ingressi 4 uscite
- Usare il decodificatore assieme al multiplexer (altra forma di multiplexer a più ingressi)
- primo Teorema della rappresentazione canonica di funzioni Booleane:
Qualunque funzione di n variabili può essere scritta univocamente come somma di j (j numero intero) prodotti di n variabili asserite o negate
o in altra forma:
Qualsiasi funzione booleana può essere espressa univocamente come somma di mintermini)
- Esempio con grafico di Venn
- Metodo per ottenere in forma canonica una funzione Booleana a partire dalla tabella di verità
- Esembio con tabella Multiplexer