Differenze tra le versioni di "Elaborazione numerica dei segnali (comdig) T1/2006-2007"
(→Lezione 1 - 2 ottobre 2006) |
(→Lezione 1 - 2 ottobre 2006) |
||
| Riga 14: | Riga 14: | ||
*'''Costante'''= un numero fisso (anche se potrebbe non essere espresso il valore) | *'''Costante'''= un numero fisso (anche se potrebbe non essere espresso il valore) | ||
*'''Variabile'''= può denotare un numero, assume valori in un determinato dominio. | *'''Variabile'''= può denotare un numero, assume valori in un determinato dominio. | ||
| − | + | '''Una variabile NON è una costante!''' | |
*'''Segnale (2)'''= funzione da un dominio a un codominio. ''Se un segnale è definito R<math>\rightarrow</math>R è un segnale continuo.'' | *'''Segnale (2)'''= funzione da un dominio a un codominio. ''Se un segnale è definito R<math>\rightarrow</math>R è un segnale continuo.'' | ||
Versione delle 21:01, 1 nov 2006
Indice
Lezione 1 - 2 ottobre 2006
- Segnale= veicolo per le informazioni, strumento. Viaggia su un canale di comunicazione. Non ha bisogno di alcuna semantica (grammatica) poichè è solo un'onda pressoria (con probabile disturbo-rumore). Inteso anche come variazione di una grandezza fisica.
Il segnale può essere rappresentato tramite una funzione (con relativi dominio e codominio).
Un'ipotetica funzione-segnale può essere la classica f:R R (funzione:dominio
R (funzione:dominio codominio), cioè una funzione che ha come dominio e come codominio una retta.
(NB: un'immagine ha come dominio il piano reale vale a dire RxR, cioè
codominio), cioè una funzione che ha come dominio e come codominio una retta.
(NB: un'immagine ha come dominio il piano reale vale a dire RxR, cioè 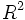 e come codominio la retta reale cioè R).
Il suono è un tipo di segnale che varia in una sola dimensione: il tempo.
e come codominio la retta reale cioè R).
Il suono è un tipo di segnale che varia in una sola dimensione: il tempo.
Considerando f:R R ed x variabile, t variabile: f(x) e f(t) hanno la stessa semantica, cioè la funzione è sempre la stessa, ha lo stesso comportamento sia su x che su t, nonostante queste ultime siano differenti.
R ed x variabile, t variabile: f(x) e f(t) hanno la stessa semantica, cioè la funzione è sempre la stessa, ha lo stesso comportamento sia su x che su t, nonostante queste ultime siano differenti.
- Costante= un numero fisso (anche se potrebbe non essere espresso il valore)
- Variabile= può denotare un numero, assume valori in un determinato dominio.
Una variabile NON è una costante!
- Segnale (2)= funzione da un dominio a un codominio. Se un segnale è definito R
 R è un segnale continuo.
R è un segnale continuo.
- Segnale continuo o analogico= è un segnale a valori continui ed a tempo continuo. Questo genere di segnale ha però valori infiniti
Come rendere FINITO il segnale?
- Campionamento= divisione del tempo in un tot di campioni, rendendo il tempo non più una serie di valori numerici infinita, ma una serie di valori finita. Il tempo diventa discreto (finito).
Il segnale campionato diventa una funzione f:Z R. Poniamo di prendere un campione
R. Poniamo di prendere un campione 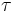 (lettera greca minuscola tau): tutti gli altri campioni saranno multipli di
(lettera greca minuscola tau): tutti gli altri campioni saranno multipli di 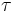 (cioè
(cioè 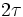 ,
, 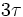 , ecc...).
Il segnale campionato si dice a tempo discreto e a valori continui: valori continui poichè, pur dividendo il segnale in campioni, fra un campione e l'altro sussistono ancora valori di segnale (infiniti).
In un'immagine (bidimensionale) dopo un campionamento avrei f:
, ecc...).
Il segnale campionato si dice a tempo discreto e a valori continui: valori continui poichè, pur dividendo il segnale in campioni, fra un campione e l'altro sussistono ancora valori di segnale (infiniti).
In un'immagine (bidimensionale) dopo un campionamento avrei f: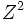
 R.
R.
- Quantizzazione= divisione della funzione (dei valori della funzione) in valori finiti: avrò, per esempio, da una serie infinita di numeri, solo "pochi" numeri (ad esempio la serie 1 2 4 6) che possono ripetersi (ad esempio la mia funzione potrà avere valori 1 2 4 6 6 6 4 1...).
Il segnale (solamente) quantizzato si dice a valori discreti e a tempo continuo.
La funzione (solamente) quantizzata è definita come f:R Z.
Z.
Se noi eseguiamo la seguante (con f:R R, quindi segnale continuo):
Segnale
R, quindi segnale continuo):
Segnale Campionamento
Campionamento Quantizzazione
Quantizzazione Segnale Digitale
otteniamo, per l'appunto, il segnale digitale, una funzione definita in Z
Segnale Digitale
otteniamo, per l'appunto, il segnale digitale, una funzione definita in Z Z, cioè a tempo discreto e a valori discreti.
Z, cioè a tempo discreto e a valori discreti.
ESERCIZIO Quanti bit sono necessari a memorizzare N valori interi? (Si prenderanno in esempio i livelli di grigio di un'immagine, cioè 256 valori)
N= 256= {0, 1, ..., 255}
Dato che 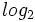 256= 8, serve 1 Byte (8 bit) per memorizzare 256 valori.
256= 8, serve 1 Byte (8 bit) per memorizzare 256 valori.
Infatti 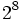 = 256.
= 256.
ESERCIZIO
Dato un certo intervallo di campionamento tau 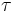 , sapendo che il reciproco di
, sapendo che il reciproco di 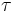 è
è  =
=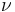 (nu): calcolare la frequenza, dato
(nu): calcolare la frequenza, dato 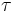 =1000.
=1000.
Troviamo  =
= 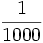 = 1 KHz
= 1 KHz
ESERCIZIO
Con un intervallo di durata T, un intervallo tra campioni 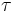 ed N valori possibili calcolare i bit necessari per rappresentare il segnale con i valori dati.
ed N valori possibili calcolare i bit necessari per rappresentare il segnale con i valori dati.
La formula è 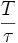
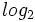 N (in bit).
N (in bit).
FINE  la.luna
la.luna per favore, se leggete errori modificate il wiki oppure segnalatemelo =)
per favore, se leggete errori modificate il wiki oppure segnalatemelo =)
Lezione 2 - 5 ottobre 2006
- Concetto di sistema
- Sistema deterministico
- Cos'è e come è composto un DSP
- ADC, DSP, DAC
- Concetto di filtro
- Le operazioni sulle funzioni (composizione, addizione, sottrazione, prodotto, prodotto per un reale)
- Variazione di scala
- Traslazione
- Funzione rettangolo Rect(t)
Lezione 3 - 9 ottobre 2006
- Funzioni trigonometriche (sin, cos, tan)
- Funzione periodica
- Operazioni con le funzioni elementari sin e cos
- Variazione di scala e traslazione con funzioni trigonometriche
- Coseno è pari
- Seno è dispari
- Esercizio su come campionare e quantizzare una funzione
Lezione 4 - 12 ottobre 2006
- Funzione Sinc(t)
- Impulso o Delta di Dirac
- Operazioni sui segnali con un sistema
- Combinazione lineare di segnali (da diversi sistemi)
Lezione 5 - 16 ottobre 2006
- Vettori
- Spazi vettoriali
- Base vettoriale
- Base ortogonale e ortonormale
- Prodotto interno
Lezione 6 - 19 ottobre 2006
- Basi ortogonali e ortonormali
- Prodotto interno coi segnali
- Vettori e segnali
- Delta Impulso Discreto
Lezione 7 - 23 ottobre 2006
- Concetto di supporto finito del segnale
- Combinazione lineare di segnali
- Complementi sulla Delta di Dirac e dimostrazione
- Sistemi lineari ed operazioni dei sistemi lineari