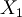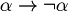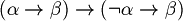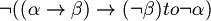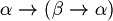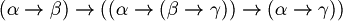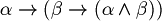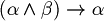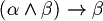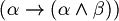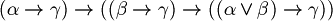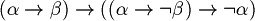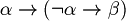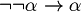Differenze tra le versioni di "Logica fuzzy"
(→Relationship between syntax and semantic) |
(→Relationship between syntax and semantic) |
||
| Riga 163: | Riga 163: | ||
It is really hard to find theorems in this way: in this course we don't have to learn this, just have to know how a formal syntactic demonstration are made. | It is really hard to find theorems in this way: in this course we don't have to learn this, just have to know how a formal syntactic demonstration are made. | ||
| − | Thanks to completeness and validity theorem we can prove theorem through an easier way; infact it says that <math>THM | + | Thanks to completeness and validity theorem we can prove theorem through an easier way; infact it says that <math>THM \equiv TAUT</math> the set of theorems and the set of tautologies coincide. |
Hence, proving that a formula is a tautology is equals to prove that a formula is a theorem. This is the bridge between Syntax and Semantic. | Hence, proving that a formula is a tautology is equals to prove that a formula is a theorem. This is the bridge between Syntax and Semantic. | ||
Versione delle 13:57, 20 ott 2012
| Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata. |
Indice
A.A. passati
Information
Course's website
Times and classrooms:
Monday 15:30 - 17:30 - Room 5 (Ground floor - via comelico 39)
Friday 10:30 - 12:30 - Room 5
Lessons' notes
This notes are written in english to help foreign students to follow this course.
Classical Propositional Logic
We are going to describe the classical propositional logic (L.P.C) language.
Syntax
The syntax of a language is the set of rules that specify how the elements of the language are formed regardless their meaning.
Let 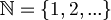 be the set of the natural numbers and
be the set of the natural numbers and 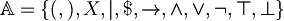 an alphabet of symbols.
an alphabet of symbols.
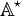 is the set of strings on this alphabet. For example
is the set of strings on this alphabet. For example 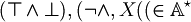 .
.
We have now to define the set of the "well formed formula" 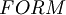 , that is the set of the elements of the L.P.C.
, that is the set of the elements of the L.P.C.
Definition (well formed formulas). 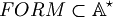 is defined with some conditions:
is defined with some conditions:
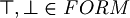
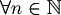
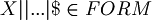 , where | is taken n times. For example:
, where | is taken n times. For example: 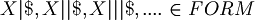
- if
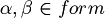 , then
, then 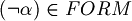 .
. - if
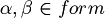 , then
, then 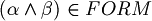 .
. - if
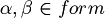 , then
, then 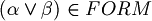 .
. - if
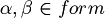 , then
, then 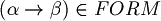 .
.
Well formed formulas is often abbreviated with f.b.f.
The strings in condition (2) are called "propositional variables" or "atomic formulas" or "propositional letters" or simply "variables". They are abbreviated with this notation:
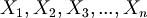 (In other books p, q, r, .., are used to refer to variables).
(In other books p, q, r, .., are used to refer to variables).
The set of variables is 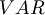 .
.
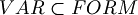
Example of well formed formulas:
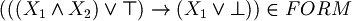
Instead
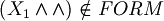
In this notes we omit (, ) where it is clear the precedence of the connectives. (Connectives are 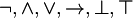 )
)
Why don't we use directly 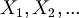 or
or 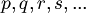 ?
?
Because it is important that the alphabet is a finited set. Although, in this notes, we use 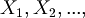 notation.
It is essential, even, that the L.P.C. language is decidable, that is it must exist an algorithm that tell us if a string is
notation.
It is essential, even, that the L.P.C. language is decidable, that is it must exist an algorithm that tell us if a string is  or not.
For this reason it is crucial the
or not.
For this reason it is crucial the
Unique readability of well formed formulas. For all 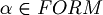 one (and only one) of the following sentences must be true:
one (and only one) of the following sentences must be true:
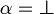 or
or 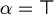 but not both.
but not both.- Exists an unique
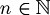 such that
such that 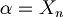 .
. - Exists an unique
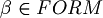 such that
such that 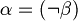 .
. - Exist unique
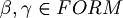 such that
such that 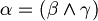 .
. - Exist unique
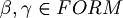 such that
such that 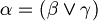 .
. - Exist unique
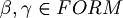 such that
such that 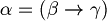 .
.
Let's, infact, consider the parser of the algorithm we talked above:
When it find, for example, 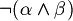 , to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if
, to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if 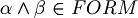 . But how can it do this? Deciding if
. But how can it do this? Deciding if 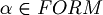 and
and 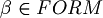 .
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
.
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
Formally, a string 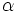 is a finite sequence of elements:
is a finite sequence of elements:
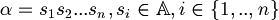
A substring of 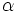 is a string in the form
is a string in the form 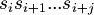 , where
, where 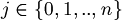 and
and  .
.
A subformula is a substring  .
.
For example:
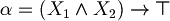
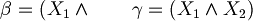
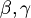 are both substring of
are both substring of 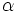 but only
but only 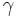 is a subformula.
With
is a subformula.
With 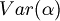 we indicate the set of variables that are subformulas of
we indicate the set of variables that are subformulas of 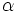 .
With
.
With 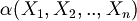 we denote a formula whose variables are a subset of
we denote a formula whose variables are a subset of 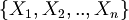 .
.
Semantic
The semantic of a language is the relation between the elements of that language and their meaning.
The set {0,1} is called truth values set. 0 means false and 1 means true.
Definition(Assignment). An atomic assignment is any function
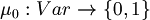 .
.
An assignment (or interpretation) is a function
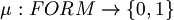
that extends 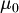 and respects the following rules for every
and respects the following rules for every 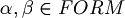 .
.
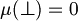 and
and 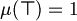
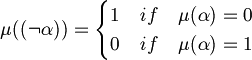
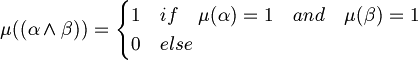
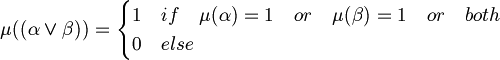
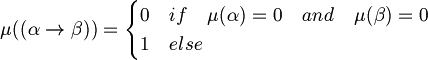
Informally we can say that the variables represent propositions with one verb and one or more complement. For example:
 "It rains";
"It rains";
 "I go to school".
"I go to school".
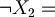 "I don't go to school"
"I don't go to school"
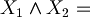 "It rains and I go to school"
"It rains and I go to school"
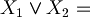 "it rains or I go to school"
"it rains or I go to school"
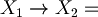 "If it rains then I will go to school"
"If it rains then I will go to school"
I can choose 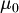 such as
such as 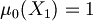 and
and 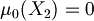
Consequently we have
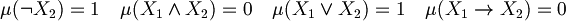
Proposition (Unique extendibility of atomic assignment): Every atomic assignment 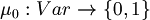 admits exactly one extension to an assignment
admits exactly one extension to an assignment 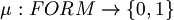
More informally, as you can see in the example above, when we choose the values of the variables we determinate the values of the formulas within those variables.
Definition (truth and falsehood). Let 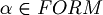 . When we have
. When we have 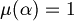 we say that
we say that 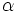 is true in the interpretation of
is true in the interpretation of 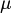 , or
, or 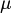 is a model of
is a model of 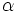 . Instead, when we have
. Instead, when we have 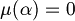 we say that
we say that 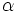 is false in the interpretation of
is false in the interpretation of 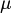 , or
, or 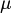 is an anti-model of
is an anti-model of 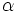 .
.
In symbols:
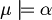 when
when 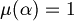
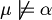 when
when 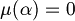 .
.
When  is true for every
is true for every  we say that
we say that  is a tautology. Instead when we have
is a tautology. Instead when we have 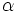 false for every assignment
false for every assignment 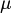 we say that
we say that 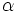 is a contradiction.
When exists a
is a contradiction.
When exists a 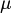 such as
such as 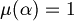 we say that
we say that 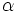 is satisfiable; instead when exists a
is satisfiable; instead when exists a 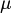 such as
such as 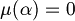 we say that
we say that 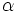 is refutable.
is refutable.
In symbols:
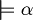 tautology
tautology
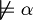 refutable
refutable
In these notes we abbreviate
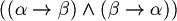
with
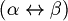
and it can be read as "if and only if".
Exercise. Prove that the following formulas are tautologies for all 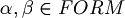
Hint: use the truth table
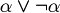
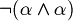
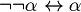
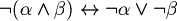 (De Morgan rule I)
(De Morgan rule I)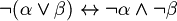 (De Morgan rule II)
(De Morgan rule II)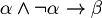
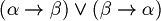
Exercise. Prove that exist 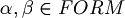 for those the following formulas aren't tautologies. Which of these are contradiction?
for those the following formulas aren't tautologies. Which of these are contradiction?
Hint: to prove that a formula isn't a tautology is sufficient an counter-example but to prove that it is a contradiction it isn't sufficient. You can use the truth table again.
Relationship between syntax and semantic
Definition (Axioms of LPC (Classical propositional logic)). For all 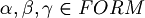 , let's consider the following formulas.
, let's consider the following formulas.
The formulas between 1 and 11 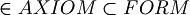 .
.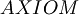 is called set of the axioms of the classical propositional logic.
is called set of the axioms of the classical propositional logic.
The cardinality of 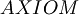 is
is 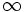 because
because 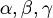 can be other formulas. For example:
can be other formulas. For example:
Let 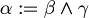 and substitute in the first axiom; it becomes
and substitute in the first axiom; it becomes
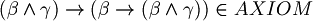
It is important to understand that the axioms are defined only through syntax, because we don't speak about values of formulas. Axioms, for definition, are demostrable without demonstration.
Think about syntax and semantic as two different worlds. In "syntax world" there are 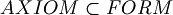 but even
but even 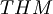 , the set of theorems. So we have
, the set of theorems. So we have
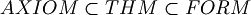
The elements of 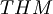 are the demonstrable formulas.
are the demonstrable formulas.
Definition. We say that a formula 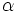 is demonstrable (or syntactic consequence),
is demonstrable (or syntactic consequence), 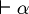 if exist a finite sequence of formulas
if exist a finite sequence of formulas 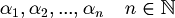 such that
such that 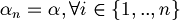 one of the following conditions is true.
one of the following conditions is true.
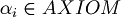
- Exist indexes
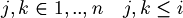 such that
such that 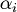 is deducible from
is deducible from 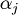 and
and 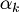 through modus ponens.
through modus ponens.
A sequence of formulas like that is a formal demonstration of 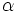 .
.
Definition (modus ponens). Let 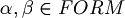 . We say that
. We say that 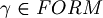 is deducible, through modus ponens, if
is deducible, through modus ponens, if 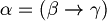 .
For example:
.
For example: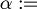 "If it rains then I will stay home"
"If it rains then I will stay home" 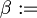 "It rains"
"It rains" 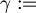 "I go to school".
We know that
"I go to school".
We know that 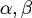 are true, hence we can say that
are true, hence we can say that 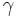 is true.
is true.
The elements of 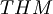 are found in this way through modus ponens starting from elements of
are found in this way through modus ponens starting from elements of 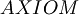 .
Modus ponens is one of the inference rules.
Example of demonstration:
We want to prove that
.
Modus ponens is one of the inference rules.
Example of demonstration:
We want to prove that 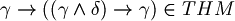 .
We start from axioms 1, 4.
.
We start from axioms 1, 4.
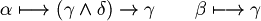 (substitution of
(substitution of 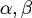 in A1 (first axiom)
in A1 (first axiom)
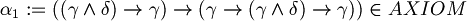
 (substitution in A4)
(substitution in A4)
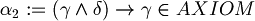 Now we have
Now we have 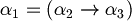 hence we can conclude that
hence we can conclude that
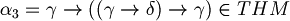
It is really hard to find theorems in this way: in this course we don't have to learn this, just have to know how a formal syntactic demonstration are made.
Thanks to completeness and validity theorem we can prove theorem through an easier way; infact it says that 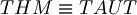 the set of theorems and the set of tautologies coincide.
Hence, proving that a formula is a tautology is equals to prove that a formula is a theorem. This is the bridge between Syntax and Semantic.
the set of theorems and the set of tautologies coincide.
Hence, proving that a formula is a tautology is equals to prove that a formula is a theorem. This is the bridge between Syntax and Semantic.
Theorem of validity and completeness. For all 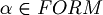 we have
we have
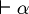 if and only if
if and only if 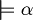
The demonstrable formulas coincide with tautologies.
Example:
If I prove that 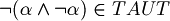 (using truth table or by reduction to absurd or any other way that use the values of the formulas (semantic)) then, it must exist a syntactical demonstration (starting from axioms and going on through modus ponens) to prove that formula.
(using truth table or by reduction to absurd or any other way that use the values of the formulas (semantic)) then, it must exist a syntactical demonstration (starting from axioms and going on through modus ponens) to prove that formula.