Differenze tra le versioni di "Metodi probabilistici/2006-2007"
(→Diario del corso) |
(→Diario del corso) |
||
| Riga 62: | Riga 62: | ||
** <math>\sigma</math>-algebra generata da un insieme di eventi | ** <math>\sigma</math>-algebra generata da un insieme di eventi | ||
** Teorema: l'intersezione di <math>\sigma</math>-algebre è una <math>\sigma</math>-algebra. | ** Teorema: l'intersezione di <math>\sigma</math>-algebre è una <math>\sigma</math>-algebra. | ||
| + | |||
| + | === Lezione del 16/3/2006 === | ||
| + | |||
| + | * <math>\sigma</math>-algebra generata dall'insieme degli intervalli sui reali. | ||
| + | * Inclusione stretta della <math>\sigma</math>-algebra generata dall'insieme degli intervalli sui reali nell'insieme delle parti dei reali ( <math>\sigma(I) \subset P(R)</math> ). | ||
| + | * Dimostrazione del fatto che i numeri normali sono un elemento della <math>\sigma</math>-algebra di Borel su [0,1]. | ||
| + | |||
| + | === Lezione del 19/3/2006 === | ||
| + | |||
| + | * Lemma di Borel-Cantelli | ||
| + | * Legge forte dei grandi numeri. | ||
| + | * Legge debole dei grandi numeri. | ||
| + | * Statistica estremale, statistica d'ordine. | ||
| + | |||
| + | === Lezione del 23/3/2006 === | ||
| + | |||
| + | * Considerazioni sulla linearità del valore atteso: dimostrazione del fatto che se X e Y sono variabili casuali, allora lo sono anche X+Y e aX (dove a è una costante). | ||
| + | * Nozione di distanza tra variabili casuali (errore quadratico medio). | ||
| + | * Tipi di convergenza: | ||
| + | ** quasi ovunque | ||
| + | ** in probabilità | ||
| + | ** in distribuzione. | ||
| + | * Statistica parametrica | ||
| + | * Stimatori, confronto tra stimatori tramite la legge dei grandi numeri. | ||
| + | |||
| + | === Lezione del 26/3/2006 === | ||
| + | |||
| + | * Costruzione della <math>\sigma</math>-algebra di Borel sui reali. | ||
| + | * Misura di Lebesgue. | ||
| + | * Definizione formale di eventi indipendenti. | ||
| + | |||
| + | === Lezione del 30/3/2006 === | ||
| + | |||
| + | * Studio congiunto di due variabili: | ||
| + | ** Costruzione della <math>\sigma</math>-algebra di Borel su <math>R^2</math> | ||
| + | ** Funzione di distribuzione e di ripartizione congiunta di due variabili. | ||
Versione delle 15:38, 1 apr 2007
News
L'orario è cambiato rispetto a quanto scritto inizialmente sul ccdi: la lezione del martedì è spostata al lunedì.
Appelli
15/1/2007 - 15/2/2007 - 23/4/2007 - 13/6/2007 - 5/7/2007 - 13/9/2007
Informazioni generali
Docenti
Diego De Falco
Corsi di laurea
Corso di laurea magistrale in Informatica
Modalità d'esame
* esame scritto del corso di Calcolo delle probabilità e statistica matematica * elaborato scritto su un tema specifico concordato con il docente durante un colloquio o in aula
Prerequisiti al corso
Preferibilmente il corso di Calcolo delle probabilità e statistica matematica (o equivalente).
Orari e luogo delle lezioni
Lunedì 8:30-10:30 aula Beta (Comelico) Venerdì 8:30-10:30 aula Beta (Comelico)
Orario di ricevimento studenti
lunedì dalle 10,30 alle 12,30 stanza P134 via Comelico 39
Materiale didattico
Testi
Mood, Graybill, Boes - Introduzione alla statistica - McGraw-Hill Bartoszyński, Niewiadomska Bugaj - Probability and statistical inference - Wiley 1996
Fotocopie
Durante le lezioni il docente mette a disposizione delle fotocopie riguardanti gli argomenti trattati
Diario del corso
Lezione del 6/3/2006
- Ripasso dei concetti fondamentali di CPSM seguendo il tema d'esame del 15/2/2007
- Variabile casuale bernoulliana e funzione indicatrice
- Insieme degli esiti, insieme degli eventi (e proprietà), spazio misurabile
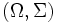 , definizione di misurabilità rispetto a
, definizione di misurabilità rispetto a 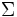
- Definizione formale di variabile casuale.
Lezione del 09/3/2006
- Ancora ripasso di CPSM
- Funzione di probabilità (e proprietà)
- Spazio di probabilità
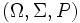
- Introduzione al valore atteso: formula per calcolarlo e definizione nel caso di variabili bernoulliane
- Definizione di variabili/eventi P-indipendenti
- Teorema: se due eventi sono indipendenti, anche i loro complementi lo sono
- Definizione di probabilità condizionata
- Concetto di simulazione
- Metodo per stabilire l'equità della ricompensa associata a una scommessa.
Lezione del 12/3/2006
- Concetti sparsi di CPSM
- Variabili indipendenti
- Variabili identicamente distribuite
- Funzione caratteristica (= generatrice dei momenti).
- Proprietà delle
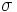 -algebre
-algebre
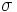 -algebra generata da un insieme di eventi
-algebra generata da un insieme di eventi- Teorema: l'intersezione di
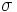 -algebre è una
-algebre è una 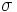 -algebra.
-algebra.
Lezione del 16/3/2006
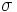 -algebra generata dall'insieme degli intervalli sui reali.
-algebra generata dall'insieme degli intervalli sui reali.- Inclusione stretta della
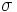 -algebra generata dall'insieme degli intervalli sui reali nell'insieme delle parti dei reali (
-algebra generata dall'insieme degli intervalli sui reali nell'insieme delle parti dei reali ( 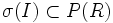 ).
). - Dimostrazione del fatto che i numeri normali sono un elemento della
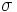 -algebra di Borel su [0,1].
-algebra di Borel su [0,1].
Lezione del 19/3/2006
- Lemma di Borel-Cantelli
- Legge forte dei grandi numeri.
- Legge debole dei grandi numeri.
- Statistica estremale, statistica d'ordine.
Lezione del 23/3/2006
- Considerazioni sulla linearità del valore atteso: dimostrazione del fatto che se X e Y sono variabili casuali, allora lo sono anche X+Y e aX (dove a è una costante).
- Nozione di distanza tra variabili casuali (errore quadratico medio).
- Tipi di convergenza:
- quasi ovunque
- in probabilità
- in distribuzione.
- Statistica parametrica
- Stimatori, confronto tra stimatori tramite la legge dei grandi numeri.
Lezione del 26/3/2006
- Costruzione della
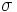 -algebra di Borel sui reali.
-algebra di Borel sui reali. - Misura di Lebesgue.
- Definizione formale di eventi indipendenti.
Lezione del 30/3/2006
- Studio congiunto di due variabili:
- Costruzione della
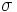 -algebra di Borel su
-algebra di Borel su 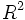
- Funzione di distribuzione e di ripartizione congiunta di due variabili.
- Costruzione della