Differenze tra le versioni di "Metodi probabilistici/2007-2008"
m (→Diario del corso: inserito codice LaTeX) |
|||
| Riga 8: | Riga 8: | ||
* Ripasso del concetto di funzione di ripartizione | * Ripasso del concetto di funzione di ripartizione | ||
** Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato | ** Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato | ||
| − | * Primo approccio al concetto di funzione misurabile (Sigma-s misurabile, con s semiretta dei Reali) | + | * Primo approccio al concetto di funzione misurabile (<math>\Sigma</math>-s misurabile, con s semiretta dei Reali <math>\mathbb{R}</math>) |
=== Lezione del giorno 7/3/2008 === | === Lezione del giorno 7/3/2008 === | ||
| − | * Recap del modello Kolmogoroviano ( | + | * Recap del modello Kolmogoroviano (<math>\Omega</math>, <math>\Sigma</math>, P) |
* Proprietà delle funzioni di ripartizione | * Proprietà delle funzioni di ripartizione | ||
** Ripasso del concetto di continuità da dx e sx | ** Ripasso del concetto di continuità da dx e sx | ||
| Riga 18: | Riga 18: | ||
** Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo". | ** Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo". | ||
*** Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti". | *** Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti". | ||
| − | ** Parallelismo tra Modello Kolmogoroviano e terna (R, B(R), Px) | + | ** Parallelismo tra Modello Kolmogoroviano e terna (<math>\mathbb{R}</math>, <math>\mathcal{B}</math>(<math>\mathbb{R}</math>), Px) |
| − | ** Prima citazione degli insieme di Borel | + | ** Prima citazione degli insieme di Borel <math>\mathcal{B}</math>(<math>\mathbb{R}</math>). |
* Ripasso del concetto di esponenziale (con naturale estensione al piano complesso) | * Ripasso del concetto di esponenziale (con naturale estensione al piano complesso) | ||
** Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x) | ** Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x) | ||
*** Ripasso del concetto di derivata come limite del rapporto incrementale | *** Ripasso del concetto di derivata come limite del rapporto incrementale | ||
*** Ricerca di una soluzione tra i polinomi | *** Ricerca di una soluzione tra i polinomi | ||
| − | *** Verifica della soluzione | + | *** Verifica della soluzione <math>\sum_{n=0}^{\infty}{\frac{x^n}{n!}}</math> |
*** Verifica della convergenza della serie | *** Verifica della convergenza della serie | ||
| − | ** Definizione formale del numero di | + | ** Definizione formale del numero di Nepero |
** Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton] | ** Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton] | ||
** Esponenziale di complessi | ** Esponenziale di complessi | ||
*** Legame con funzione seno e coseno | *** Legame con funzione seno e coseno | ||
Versione delle 07:45, 8 mar 2008
Diario del corso
Lezione del giorno 3/3/2008
- Introduzione al corso
- Partendo dal concetto di variabile casuale ripasso di:
- Funzione, Relazione, Prodotto Cartesiano
- Ripasso del concetto di funzione di ripartizione
- Ri-defizione del concetto di funzione di ripartizione come probabilità della controimmagine di una variabile casuale con argomento la semiretta dei reali delimitata da un x segnato
- Primo approccio al concetto di funzione misurabile (
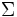-s misurabile, con s semiretta dei Reali 
)
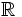Lezione del giorno 7/3/2008
- Recap del modello Kolmogoroviano (
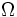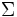, , P) - Proprietà delle funzioni di ripartizione
- Ripasso del concetto di continuità da dx e sx
- Data una generica F(x) che gode delle tre proprietà (MGB 67-68) questa è una funzione di ripartizione della quale possiamo definire modello Kolmogoroviano. (Vedi MGB 68-2.3)
- Concetto di misurabilità partendo da esempi elementari (da CPSM) con distribuzione uniforme in (a,b]
- Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo".
- Non tutti i sottoinsiemi di una retta R sono intervalli, eppure sono "interessanti".
- Parallelismo tra Modello Kolmogoroviano e terna (,
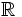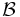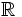(), Px) - Prima citazione degli insieme di Borel ().
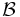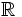- Il concetto di misurabilità va ridefinito superando il "vincolo dell'intervallo".
- Ripasso del concetto di esponenziale (con naturale estensione al piano complesso)
- Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x)
- Ripasso del concetto di derivata come limite del rapporto incrementale
- Ricerca di una soluzione tra i polinomi
- Verifica della soluzione
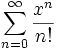
- Verifica della convergenza della serie
- Definizione formale del numero di Nepero
- Cenno di dimostrazione sulla proprietà exp(x+y) = exp(x) * exp(y) [utilizzare binomio di Newton]
- Esponenziale di complessi
- Legame con funzione seno e coseno
- Sistema di 2 equazioni g(0) = 1 , g'(x) = g(x)
