Logica fuzzy

Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata.

A.A. passati

• (Marra, Aguzzoli), A.A. 2007-2008

Information

Course's website
Times and classrooms:
Monday 15:30 - 17:30 - Room 5 (Ground floor - via comelico 39)
Friday 10:30 - 12:30 - Room 5

Lessons' notes

This notes are written in english to help foreign students to follow this course.

Classical Propositional Logic

Lesson 1 - 5th october

In this lesson we are going to describe the classical propositional logic (L.P.C) language.

Sintax

Let's 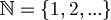${\mathbb {N}}=\{1,2,...\}$ be the set of the natural numbers and 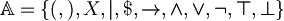${\mathbb {A}}=\{(,),X,|,\$,\rightarrow ,\land ,\lor ,\neg ,\top ,\bot \}$ an alphabet of symbols.
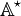${\mathbb {A}}^{\star }$ is the set of strings on this alphabet. For example $(\top \land \bot ),(\neg \land ,...,X((\in {\mathbb {A}}^{\star }$.
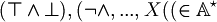We have now to define the set of the "well formed formula" 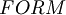$FORM$, that is the set of the element of the L.P.C.
Definition (well formed formulas). 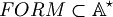$FORM\subset {\mathbb {A}}^{\star }$ is defined with some conditions:

1. $\top ,\bot \in FORM$
2. $\forall n\in {\mathbb {N}}$
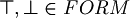
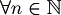
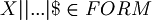   $\qquad X||...|\$\in FORM$, where | is taken n times. For example: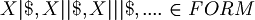 $X|\$,X||\$,X|||\$,....\in FORM$
3. if 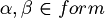$\alpha ,\beta \in form$, then $(\neg \alpha )\in FORM$.
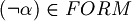4. if 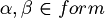$\alpha ,\beta \in form$, then $(\alpha \land \beta )\in FORM$.
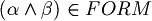5. if 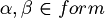$\alpha ,\beta \in form$, then $(\alpha \lor \beta )\in FORM$.
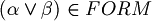6. if 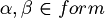$\alpha ,\beta \in form$, then $(\alpha \rightarrow \beta )\in FORM$.

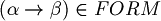Well formed formulas is often abbreviated with f.b.f. The strings in condition (2) are called "propositional variable" or "atomic formula" or "propositional letter" or simply "variable". They are abbreviated with this notation: $X_{1},X_{2},X_{3},...,X_{n}$.
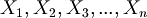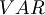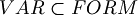
The set of variables is $VAR$.
$VAR\subset FORM$
Example of well formed formulas:
$(((X_{1}\land X_{2})\lor \top )\rightarrow (X_{1}\lor \bot ))\in FORM$
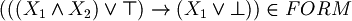
Instead
$(X_{1}\land \land )\notin FORM$

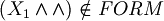
Giudizio sul corso

I giudizi di seguito espressi sono il parere personale degli studenti,
e potrebbero non rispecchiare il parere medio dei frequentanti.
Non vi è comunque alcun intento di mettere alla gogna i docenti del corso!

Interesse della materia (da 1 a 5 - aiuto)

____________________

Difficoltà del corso (da 1 a 5 - aiuto)

____________________

Difficoltà del corso per non frequentanti (da 1 a 5 - aiuto)

____________________

Ore di studio richieste (da 1 a 5 - aiuto)

____________________