Differenze tra le versioni di "Logica fuzzy"
(→Syntax) |
(→Syntax) |
||
| Riga 16: | Riga 16: | ||
In this lesson we are going to describe the classical propositional logic (L.P.C) language. | In this lesson we are going to describe the classical propositional logic (L.P.C) language. | ||
====Syntax==== | ====Syntax==== | ||
| − | Let | + | Let <math>\mathbb{N} = \{1, 2, ... \} </math> be the set of the natural numbers and <math>\mathbb{A} = \{ (, ), X, |, $, \rightarrow, \and, \or, \neg, \top, \bot \}</math> an alphabet of symbols.<br> |
<math>\mathbb{A}^\star</math> is the set of strings on this alphabet. For example <math>(\top \and \bot) , (\neg \and , X(( \in \mathbb{A}^\star</math>.<br> | <math>\mathbb{A}^\star</math> is the set of strings on this alphabet. For example <math>(\top \and \bot) , (\neg \and , X(( \in \mathbb{A}^\star</math>.<br> | ||
We have now to define the set of the "well formed formula" <math>FORM</math>, that is the set of the elements of the L.P.C.<br> | We have now to define the set of the "well formed formula" <math>FORM</math>, that is the set of the elements of the L.P.C.<br> | ||
Versione delle 19:54, 13 ott 2012
| Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata. |
Indice
[nascondi]A.A. passati
Information
Course's website
Times and classrooms:
Monday 15:30 - 17:30 - Room 5 (Ground floor - via comelico 39)
Friday 10:30 - 12:30 - Room 5
Lessons' notes
This notes are written in english to help foreign students to follow this course.
Classical Propositional Logic
Lesson 1 - 5th october
In this lesson we are going to describe the classical propositional logic (L.P.C) language.
Syntax
Let 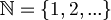 be the set of the natural numbers and
be the set of the natural numbers and 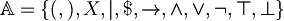 an alphabet of symbols.
an alphabet of symbols.
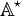 is the set of strings on this alphabet. For example
is the set of strings on this alphabet. For example 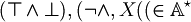 .
.
We have now to define the set of the "well formed formula" 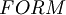 , that is the set of the elements of the L.P.C.
, that is the set of the elements of the L.P.C.
Definition (well formed formulas). 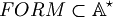 is defined with some conditions:
is defined with some conditions:
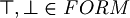
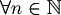
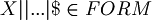 , where | is taken n times. For example:
, where | is taken n times. For example: 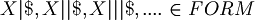
- if
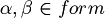 , then
, then 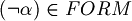 .
. - if
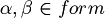 , then
, then 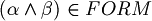 .
. - if
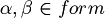 , then
, then 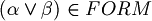 .
. - if
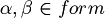 , then
, then 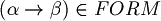 .
.
Well formed formulas is often abbreviated with f.b.f.
The strings in condition (2) are called "propositional variable" or "atomic formulas" or "propositional letters" or simply "variables". They are abbreviated with this notation:
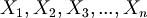 (In other books p, q, r, .., are used to refer to variables).
(In other books p, q, r, .., are used to refer to variables).
The set of variables is 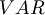 .
.
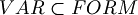
Example of well formed formulas:
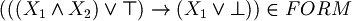
Instead
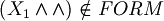
In this notes we omit (, ) where it is clear the precedence of the connectives. (Connectives are 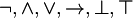 )
)
Why don't we use directly 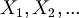 or
or 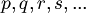 ?
?
Because it is important that the alphabet is a finited set. Although, in this notes, we use 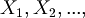 notation.
It is essential, even, that the L.P.C. language is decidability, that is it must exist an algorithm that tell us if a string is
notation.
It is essential, even, that the L.P.C. language is decidability, that is it must exist an algorithm that tell us if a string is  or not.
For this reason it is crucial the
or not.
For this reason it is crucial the
Unique readability of well formed formulas. For all 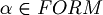 one (and only one) of the following sentences must be true:
one (and only one) of the following sentences must be true:
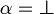 or
or 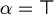 but not both.
but not both.- Exists an unique
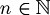 such that
such that 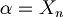 .
. - Exists an unique
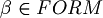 such that
such that 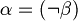 .
. - Exist unique
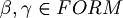 such that
such that 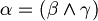 .
. - Exist unique
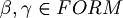 such that
such that 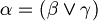 .
. - Exist unique
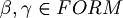 such that
such that 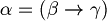 .
.
Let's, infact, consider the parser of the algorithm we talked above:
When it find, for example, 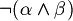 , to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if
, to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if 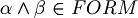 . But how can it do this? Deciding if
. But how can it do this? Deciding if 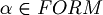 and
and 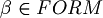 .
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
.
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
Formally, a string 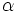 is a finite sequence of elements:
is a finite sequence of elements:
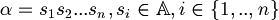
A substring of 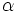 is a string in the form
is a string in the form 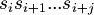 , where
, where 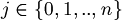 and
and  .
.
A subformula is a substring  .
.
For example:
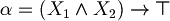
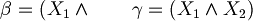
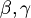 are both substring of
are both substring of 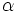 but only
but only 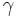 is a subformula.
With
is a subformula.
With 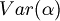 we indicate the set of variables that are subformulas of
we indicate the set of variables that are subformulas of 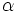 .
With
.
With 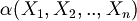 we denote a formula whose variables are a subset of
we denote a formula whose variables are a subset of 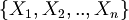 .
.
Giudizio sul corso
I giudizi di seguito espressi sono il parere personale degli studenti, e potrebbero non rispecchiare il parere medio dei frequentanti. Non vi è comunque alcun intento di mettere alla gogna i docenti del corso!
