Logica fuzzy
| Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata. |
Indice
A.A. passati
Information
Course's website
Times and classrooms:
Monday 15:30 - 17:30 - Room 5 (Ground floor - via comelico 39)
Friday 10:30 - 12:30 - Room 5
Lessons' notes
This notes are written in english to help foreign students to follow this course.
Classical Propositional Logic
We are going to describe the classical propositional logic (L.P.C) language.
Syntax
The syntax of a language is the set of rules that specify how the elements of the language are formed regardless their meaning.
Let 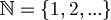 be the set of the natural numbers and
be the set of the natural numbers and 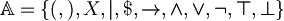 an alphabet of symbols.
an alphabet of symbols.
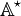 is the set of strings on this alphabet. For example
is the set of strings on this alphabet. For example 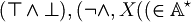 .
.
We have now to define the set of the "well formed formula" 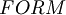 , that is the set of the elements of the L.P.C.
, that is the set of the elements of the L.P.C.
Definition (well formed formulas). 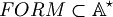 is defined with some conditions:
is defined with some conditions:
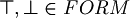
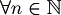
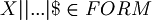 , where | is taken n times. For example:
, where | is taken n times. For example: 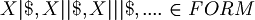
- if
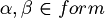 , then
, then 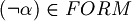 .
. - if
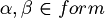 , then
, then 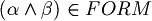 .
. - if
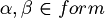 , then
, then 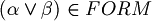 .
. - if
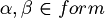 , then
, then 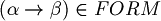 .
.
Well formed formulas is often abbreviated with f.b.f.
The strings in condition (2) are called "propositional variables" or "atomic formulas" or "propositional letters" or simply "variables". They are abbreviated with this notation:
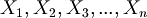 (In other books p, q, r, .., are used to refer to variables).
(In other books p, q, r, .., are used to refer to variables).
The set of variables is 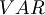 .
.
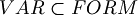
Example of well formed formulas:
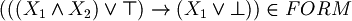
Instead
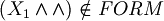
In this notes we omit (, ) where it is clear the precedence of the connectives. (Connectives are 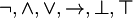 )
)
Why don't we use directly 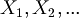 or
or 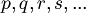 ?
?
Because it is important that the alphabet is a finited set. Although, in this notes, we use 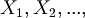 notation.
It is essential, even, that the L.P.C. language is decidable, that is it must exist an algorithm that tell us if a string is
notation.
It is essential, even, that the L.P.C. language is decidable, that is it must exist an algorithm that tell us if a string is 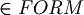 or not.
For this reason it is crucial the
or not.
For this reason it is crucial the
Unique readability of well formed formulas. For all 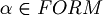 one (and only one) of the following sentences must be true:
one (and only one) of the following sentences must be true:
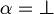 or
or 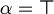 but not both.
but not both.- Exists an unique
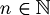 such that
such that 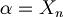 .
. - Exists an unique
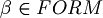 such that
such that 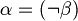 .
. - Exist unique
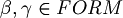 such that
such that 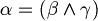 .
. - Exist unique
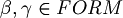 such that
such that 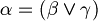 .
. - Exist unique
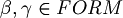 such that
such that 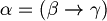 .
.
Let's, infact, consider the parser of the algorithm we talked above:
When it find, for example, 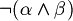 , to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if
, to decide if the string belongs to FORM, it have to decide (for the unique readability of well formed formulas) if 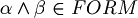 . But how can it do this? Deciding if
. But how can it do this? Deciding if 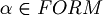 and
and 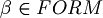 .
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
.
This is what the above theorem tell us. Try to draw the parser tree. It is unique thanks to, again, that theorem.
Formally, a string 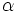 is a finite sequence of elements:
is a finite sequence of elements:
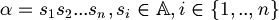
A substring of 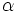 is a string in the form
is a string in the form 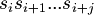 , where
, where 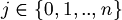 and
and  .
.
A subformula is a substring 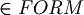 .
.
For example:
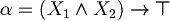
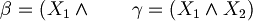
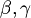 are both substring of
are both substring of 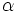 but only
but only 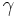 is a subformula.
With
is a subformula.
With 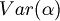 we indicate the set of variables that are subformulas of
we indicate the set of variables that are subformulas of 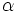 .
With
.
With 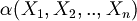 we denote a formula whose variables are a subset of
we denote a formula whose variables are a subset of 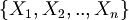 .
.
Semantic
The semantic of a language is the relation between the elements of that language and their meaning.
The set {0,1} is called truth values set. 0 means false and 1 means true.
Definition(Assignment). An atomic assignment is any function
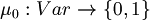 .
.
An assignment (or interpretation) is a function
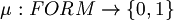
that extends 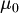 and respects the following rules for every
and respects the following rules for every 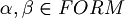 .
.
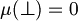 and
and 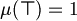
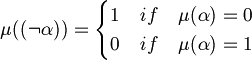
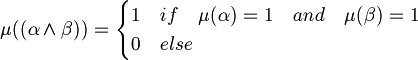
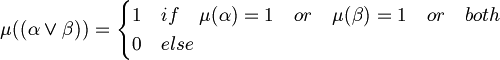
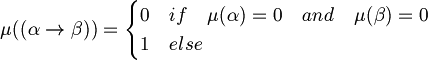
Informally we can say that the variables represent propositions with one verb and one or more complement. For example:
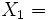 "It rains";
"It rains";
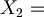 "I go to school".
"I go to school".
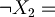 "I don't go to school"
"I don't go to school"
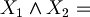 "It rains and I go to school"
"It rains and I go to school"
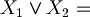 "it rains or I go to school"
"it rains or I go to school"
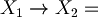 "If it rains I will go to school"
"If it rains I will go to school"
I can choose 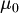 such as
such as 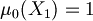 and
and 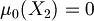
Consequently we have
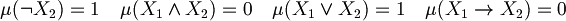
Proposition (Inique extendibility of atomic assignment): Every atomic assignment 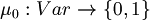 admits exactly one extension to an assignment
admits exactly one extension to an assignment 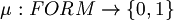
More informally, as you can see in the example above, when we choose the values of the variables we determinate the values of the formulas within those variables.
Definition (truth and falsehood). Let 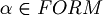 . When we have
. When we have 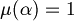 we say that
we say that 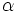 is true in the interpretation of
is true in the interpretation of 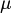 , or
, or 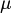 is a model of
is a model of 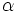 . Instead, when we have
. Instead, when we have 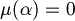 we say that
we say that 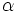 is false in the interpretation of
is false in the interpretation of 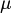 , or
, or 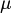 is an anti-model of
is an anti-model of 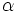 .
.
In symbols:
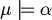 when
when 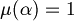
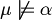 when
when 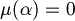 .
.
When 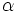 is true for every
is true for every 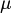 we say that
we say that 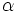 is a tautology. Instead when we have
is a tautology. Instead when we have 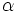 false for every assignment
false for every assignment 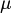 we say that
we say that 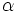 is a contradiction.
When exists a
is a contradiction.
When exists a 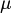 such as
such as 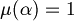 we say that
we say that 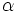 is satisfiable; instead when exists a
is satisfiable; instead when exists a 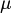 such as
such as 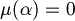 we say that
we say that 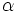 is refutable.
is refutable.
In symbols:
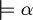 tautology
tautology
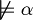 refutable
refutable
