Elaborazione numerica dei segnali (comdig) T1/2006-2007
Indice
- 1 INFORMAZIONI GENERALI
- 2 Lezione 1 - 2 ottobre 2006
- 3 Lezione 2 - 5 ottobre 2006
- 4 Lezione 3 - 9 ottobre 2006
- 5 Lezione 4 - 12 ottobre 2006
- 6 Lezione 5 - 16 ottobre 2006
- 7 Lezione 6 - 19 ottobre 2006
- 8 Lezione 7 - 23 ottobre 2006
- 9 Lezione 8 - 30 ottobre 2006
- 10 Lezione 9 - 2 novembre 2006
- 11 Lezione 10 - 7 novembre 2006
- 12 Lezione 11 - 9 novembre 2006
- 13 Lezione 12 - 13 novembre 2006
INFORMAZIONI GENERALI
- Docente: Paola Campadelli
- Luogo ed orario: LUN 8.45-10.30 aula 405, GIO 10.30-12.30 aula G24
- Sito del professore
- Info sul professore (webcen)
- Dispensa
Lezione 1 - 2 ottobre 2006
- Segnale= veicolo per le informazioni, strumento. Viaggia su un canale di comunicazione. Non ha bisogno di alcuna semantica (grammatica) poichè è solo un'onda pressoria (con probabile disturbo-rumore). Inteso anche come variazione di una grandezza fisica.
Il segnale può essere rappresentato tramite una funzione (con relativi dominio e codominio).
Un'ipotetica funzione-segnale può essere la classica f:R R (funzione:dominio
R (funzione:dominio codominio), cioè una funzione che ha come dominio e come codominio una retta.
(NB: un'immagine ha come dominio il piano reale vale a dire RxR, cioè
codominio), cioè una funzione che ha come dominio e come codominio una retta.
(NB: un'immagine ha come dominio il piano reale vale a dire RxR, cioè 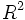 e come codominio la retta reale cioè R).
Il suono è un tipo di segnale che varia in una sola dimensione: il tempo.
e come codominio la retta reale cioè R).
Il suono è un tipo di segnale che varia in una sola dimensione: il tempo.
Considerando f:R R ed x variabile, t variabile: f(x) e f(t) hanno la stessa semantica, cioè la funzione è sempre la stessa, ha lo stesso comportamento sia su x che su t, nonostante queste ultime siano differenti.
R ed x variabile, t variabile: f(x) e f(t) hanno la stessa semantica, cioè la funzione è sempre la stessa, ha lo stesso comportamento sia su x che su t, nonostante queste ultime siano differenti.
- Costante= un numero fisso (anche se potrebbe non essere espresso il valore)
- Variabile= può denotare un numero, assume valori in un determinato dominio.
Una variabile NON è una costante!
- Segnale (2)= funzione da un dominio a un codominio. Se un segnale è definito R
 R è un segnale continuo.
R è un segnale continuo.
- Segnale continuo o analogico= è un segnale a valori continui ed a tempo continuo. Questo genere di segnale ha però valori infiniti
Come rendere FINITO il segnale?
- Campionamento= divisione del tempo in un tot di campioni, rendendo il tempo non più una serie di valori numerici infinita, ma una serie di valori finita. Il tempo diventa discreto (finito).
Il segnale campionato diventa una funzione f:Z R. Poniamo di prendere un campione
R. Poniamo di prendere un campione 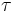 (lettera greca minuscola tau): tutti gli altri campioni saranno multipli di
(lettera greca minuscola tau): tutti gli altri campioni saranno multipli di 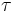 (cioè
(cioè 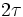 ,
, 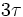 , ecc...).
Il segnale campionato si dice a tempo discreto e a valori continui: valori continui poichè, pur dividendo il segnale in campioni, fra un campione e l'altro sussistono ancora valori di segnale (infiniti).
In un'immagine (bidimensionale) dopo un campionamento avrei f:
, ecc...).
Il segnale campionato si dice a tempo discreto e a valori continui: valori continui poichè, pur dividendo il segnale in campioni, fra un campione e l'altro sussistono ancora valori di segnale (infiniti).
In un'immagine (bidimensionale) dopo un campionamento avrei f: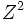
 R.
R.
- Quantizzazione= divisione della funzione (dei valori della funzione) in valori finiti: avrò, per esempio, da una serie infinita di numeri, solo "pochi" numeri (ad esempio la serie 1 2 4 6) che possono ripetersi (ad esempio la mia funzione potrà avere valori 1 2 4 6 6 6 4 1...).
Il segnale (solamente) quantizzato si dice a valori discreti e a tempo continuo.
La funzione (solamente) quantizzata è definita come f:R Z.
Z.
Se noi eseguiamo la seguante (con f:R R, quindi segnale continuo):
Segnale
R, quindi segnale continuo):
Segnale Campionamento
Campionamento Quantizzazione
Quantizzazione Segnale Digitale
otteniamo, per l'appunto, il segnale digitale, una funzione definita in Z
Segnale Digitale
otteniamo, per l'appunto, il segnale digitale, una funzione definita in Z Z, cioè a tempo discreto e a valori discreti.
Z, cioè a tempo discreto e a valori discreti.
ESERCIZIO Quanti bit sono necessari a memorizzare N valori interi? (Si prenderanno in esempio i livelli di grigio di un'immagine, cioè 256 valori)
N= 256= {0, 1, ..., 255}
Dato che 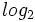 256= 8, serve 1 Byte (8 bit) per memorizzare 256 valori.
256= 8, serve 1 Byte (8 bit) per memorizzare 256 valori.
Infatti 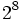 = 256.
= 256.
ESERCIZIO
Dato un certo intervallo di campionamento tau 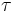 , sapendo che il reciproco di
, sapendo che il reciproco di 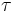 è
è  =
=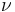 (nu): calcolare la frequenza, dato
(nu): calcolare la frequenza, dato 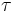 =1000.
=1000.
Troviamo  =
= 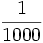 = 1 KHz
= 1 KHz
ESERCIZIO
Con un intervallo di durata T, un intervallo tra campioni 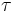 ed N valori possibili calcolare i bit necessari per rappresentare il segnale con i valori dati.
ed N valori possibili calcolare i bit necessari per rappresentare il segnale con i valori dati.
La formula è 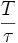
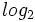 N (in bit).
N (in bit).
Lezione 2 - 5 ottobre 2006
ESERCIZIO Abbiamo 3 minuti di musica campionata a 40'000 Hz. Prendo 256 valori per campione. Quanti bit ho?
3x60 sec x40'000x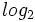 256= 57'600'000
256= 57'600'000
Considerazione: se nel logaritmo mi dovesse venire un numero indeciso (ad es 7,3) prendo comunque il numero arrotondato per eccesso (ad es 8).
- Sistema= qualsiasi dispositivo che prenda un segnale in ingresso e che produca in uscita un segnale differente.
- Sistema deterministico= un sistema nel quale non venga mai cambiato il comportamento, nonostante l'input differente.
- DSP= Digital Signal Processor, strumento usato per realizzare nel modo più efficiente possibile un sistema. Prende in input un segnale continuo e lo immette in un blocco chiamato ADC (Analog to Digital Converter) trasformando il segnale da analogico a digitale.
- ADC= costituito da un campionatore, da un quantizzatore e da un filtro iniziale (filtro di input).
- DAC= Digital to Analog Converter.
Se anche noi ipotizzassimo di inviare un ipotetico segnale f(t) all'interno di un ADC DSP
DSP DAC, in uscita non avremo mai di nuovo f(t), bensì un segnale g(t) simile a f ma mai uguale. Infatti, ADC fa perdere informazioni del segnale e crea quindi un segnale distorto.
DAC, in uscita non avremo mai di nuovo f(t), bensì un segnale g(t) simile a f ma mai uguale. Infatti, ADC fa perdere informazioni del segnale e crea quindi un segnale distorto.
- Filtro= elimina alcune informazioni.
Operazioni con le funzioni - il caso analogico
- Addizione= f(t)+g(t)
- Sottrazione= f(t)-g(t)
- Prodotto= f(t)g(t)
- Moltiplicazione per un reale= af(t), :a
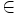 R. Fa in modo di cambiare tutti i valori della funzione.
R. Fa in modo di cambiare tutti i valori della funzione. - Composizione= f(g(t)) oppure f
 g. Viene applicata prima la funzione g(t) (per semplicità poniamolo =y) e dopodichè viene applicata f(y).
g. Viene applicata prima la funzione g(t) (per semplicità poniamolo =y) e dopodichè viene applicata f(y). - Variazione di scala=f(at). La funzione si dilata o si comprime.
- Traslazione= f(t-k), :k
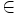 R. Contrariamente a quello che si potrebbe pensare, quando la traslazione è a -k, la funzione si sposta (sul piano delle x) verso destra, mentre se è a +k allora si sposta verso sinistra.
R. Contrariamente a quello che si potrebbe pensare, quando la traslazione è a -k, la funzione si sposta (sul piano delle x) verso destra, mentre se è a +k allora si sposta verso sinistra.
NB. Purtroppo, ma solo per il momento, non sono disponibili esempi grafici.
- La funzione rettangolo rect(t)= E' una funzione che vale 1 se x
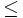 1/2, e 0 altrimenti. Dal punto di vista grafico, è un rettangolo di altezza 1 che ha metà del suo "corpo" a destra dell'asse delle y e metà a sinistra, ed è poggiato (ha la base poggiata) sull'asse x. La base di questo rettangolo è lunga a ed ha i due lati di altezza 1 nelle posizioni -a/2 ed a/2 (sull'asse x ovviamente).
1/2, e 0 altrimenti. Dal punto di vista grafico, è un rettangolo di altezza 1 che ha metà del suo "corpo" a destra dell'asse delle y e metà a sinistra, ed è poggiato (ha la base poggiata) sull'asse x. La base di questo rettangolo è lunga a ed ha i due lati di altezza 1 nelle posizioni -a/2 ed a/2 (sull'asse x ovviamente).
La Rect è importante per quanto riguarda i trattamenti sui segnali perchè posso, facendo f(t)rect(t) otteniamo un "pezzo" della funzione f(t) compreso nella regione di piano della rect(t) (ritagiando quindi il segnale).
A rect((t-b)/a) è una funzione rettangolo di ampiezza A, centrato in b (traslato) con base a.
Lezione 3 - 9 ottobre 2006
Parte grafica riguardante le funzioni trigonometriche seno e coseno (circonferenza in radianti o gradi).
- Funzione periodica= f(t) è periodica di un periodo T se f(t)=f(t+T), cioè se si ripete uguale dopo il periodo T.
Se f(t) è una funzione periodica di periodo T la funzione g(t)=f(at) (cioè variata di scala) ha periodo T'=T/a. DIMOSTRAZIONE: g(t)=f(at) per definizioe. g(t+T')=g(t). f(a(t+T'))=f(at) applico la definizione. f(at+aT')=f(at) f è periodica di t quindi aT'=T quindi T'=T/a.
Per trovare la frequenza espressa in cicli al secondo o in radianti:
Funzione - Periodo - Freq in cicli/sec - Freq in radianti
sen (t) - 2 - 1/2
- 1/2 - 1
- 1
sen (2 t) - 2
t) - 2 /2
/2 = 1 - 1 -2
= 1 - 1 -2
sen (10 t) - 1/5 - 5 - 10
t) - 1/5 - 5 - 10 = 5x2
= 5x2
sen (1/2t) - 4 - 1/4
- 1/4 - 1/2
- 1/2
NB: 1 Hz= 2 rad/sec. 1 rad/sec= 1/2
rad/sec. 1 rad/sec= 1/2 Hz.
Hz.
f(t)= A sen (2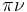 t +
t + 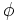 ), con
), con 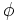 angolo (fase istantanea) ed f periodica.
angolo (fase istantanea) ed f periodica.
Esercizi ed esempi grafici non disponibili.
ESERCIZIO
f(t)= 2sen(t) se 0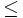 t
t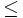 3
3 e 0 altrimenti.
CAMPIONARLA ad un intervallo di campionamento
e 0 altrimenti.
CAMPIONARLA ad un intervallo di campionamento  /2 (il nostro
/2 (il nostro 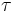 ).
QUANTIZZARLA con 3 valori per campione.
).
QUANTIZZARLA con 3 valori per campione.
Campionando f(n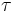 ) = [f(0), f(1x
) = [f(0), f(1x /2), f(2x
/2), f(2x /2), f(3x
/2), f(3x /2), f(4x
/2), f(4x /2), f(5x
/2), f(5x /2), f(6
/2), f(6 /2)] Vettore
/2)] Vettore
Quindi campionando ho 3 /(
/( /2)= 6 campioni più lo 0.
La funzione campionata a
/2)= 6 campioni più lo 0.
La funzione campionata a  /4 sarebbe stato ancora meglio (avrei preso il doppio dei campioni e perciò avrei un segnale più preciso!).
/4 sarebbe stato ancora meglio (avrei preso il doppio dei campioni e perciò avrei un segnale più preciso!).
Ora quantiziamo con 3 valori per campione. Fortunatamente con 3 valori non ha problemi: f(0)= 0, f( /2)= 2, f(
/2)= 2, f( )= 0, f(3/2
)= 0, f(3/2 )= -2, f(2
)= -2, f(2 )= 0, f(5/2
)= 0, f(5/2 )= 2, f(3
)= 2, f(3 )= 0.
Quindi posso utilizzare 0, -2 e 2 e non avere perdita. (Poniamo di aver quantizzato con i 3 valori ma di avere campionato a
)= 0.
Quindi posso utilizzare 0, -2 e 2 e non avere perdita. (Poniamo di aver quantizzato con i 3 valori ma di avere campionato a  /4. Avrei avuto perdita perchè avrei dovuto approssimare maggiormente e il segnale sarebbe cambiato molto).
/4. Avrei avuto perdita perchè avrei dovuto approssimare maggiormente e il segnale sarebbe cambiato molto).
Lezione 4 - 12 ottobre 2006
- Funzione sinc(t)= sinc (t)= sen(
 t)/
t)/ t, è una funzione che oscilla perchè ha sen al nominatore ma quando t aumenta il valore della funzione diminuisce. Per ogni valore di t intero ho 0. Invece, in t=0 ho il valore della funzione pari a 1. Inoltre la funzione è simmetrica, cioè sinc(t)=sinc(-t). E' inoltre limitata e continua.
t, è una funzione che oscilla perchè ha sen al nominatore ma quando t aumenta il valore della funzione diminuisce. Per ogni valore di t intero ho 0. Invece, in t=0 ho il valore della funzione pari a 1. Inoltre la funzione è simmetrica, cioè sinc(t)=sinc(-t). E' inoltre limitata e continua.
- Impulso o Delta di Dirac
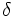 (t)=
(t)= 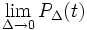 dove
dove 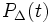 =1/
=1/ rect(t/
rect(t/ ). La Delta di Dirac ha sempre area 1, poichè, dal punto di vista grafico, è un rettangolo con una base che tende a 0 (piccolissima) ed un'altezza sempre più alta (proprio perchè mantiene l'area uguale a 1). Infatti,
). La Delta di Dirac ha sempre area 1, poichè, dal punto di vista grafico, è un rettangolo con una base che tende a 0 (piccolissima) ed un'altezza sempre più alta (proprio perchè mantiene l'area uguale a 1). Infatti, 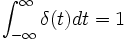 .
.
Spesso l'impulso viene rappresentato con una freccia verso l'alto sulle x (in posizione dell'eventuale traslazione).
Operazioni sui segnali
Le operazioni sui segnali vengono fatte attraverso i sistemi, che possono effettuare tutte le operazioni che abbiamo visto: amplificazione (Af(t)), traslazione (f(t-k) o f(t+k)), campionamento (f(n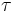 )) e la quantizzazione (argmin|x-y|).
)) e la quantizzazione (argmin|x-y|).
I sistemi possono essere composti come le funzioni, e con più segnali posso generalizzare il comportamento di segnali composti tramite una
- combinazione lineare:
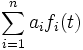 .
.
L'operazione di composizione non è sempre commutativa, mentre traslazione ed amplificazione lo sono. Scalatura e traslazione non sono commutative.
Considereremo i segnali come dei vettori.
Lezione 5 - 16 ottobre 2006
Proprietà di uno spazio vettoriale: ( , ): VxV R
R
- (v1,v)
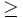 0
0 - (v1,v2)=(v2,v1)
- (av1+bv2, v3)=a(v1,v3)+b(v2,v3)
(Parte mancante...)
Lezione 6 - 19 ottobre 2006
Due vettori v1 e v2 sono
- Ortogonali se (v1,v2)=0, cioè se il loro prodotto interno è 0.
- Base= è un insieme, dato uno spazio di grandezza n, di vettori linearmente indipendenti {v1, v2,... vn}.
- Base ortogonale= quando tutti i vettori della base sono tra loro ortogonali a coppie cioè ho (vi, vj)=0 oppure norma pari a 1.
ESEMPIO
Il prodotto interno di {(1,0), (0,1)}= 1x0 + 0x1= 0.
La norma è 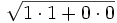 = 1 cioè del prodotto interno del vettore con se stesso.
= 1 cioè del prodotto interno del vettore con se stesso.
ESERCIZIO
Consideriamo lo spazio vettoriale di 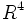 e il vettore (2, 5, 3, 7).
Voglio trovare la norma e l'angolo rispetto al vettore (1, 0, 0, 0).
e il vettore (2, 5, 3, 7).
Voglio trovare la norma e l'angolo rispetto al vettore (1, 0, 0, 0).
Norma |(2, 5, 3, 7)|= 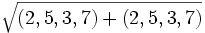 =
= 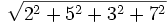 L'angolo lo calcolo dalla formula (v1, v2)= |v1||v2|cos
L'angolo lo calcolo dalla formula (v1, v2)= |v1||v2|cos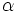 da cui cos
da cui cos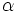 = (v1, v2)/|v1||v2|.
= (v1, v2)/|v1||v2|.
Se V è uno spazio vettoriale a dimensione finita e {v1,...vn} è una base ortogonale per V allora per ogni vettore v che appartiene a V posso scrivere v come combinazione lineare degli elementi della base v= 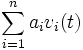 dove vi è l'elemento della base. L'elemento
dove vi è l'elemento della base. L'elemento 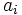 lo posso scrivere come (v, vi)/(vi, vi) (prodotto interno con la base diviso il prodotto interno del vettore con se stesso). Se la base è ortonormale ciò significa che gli elementi della base sono a 1 quindi non c'è denominatore.
Se ho un vettore e una base posso comunque calcolare i coefficienti della base ortogonale.
lo posso scrivere come (v, vi)/(vi, vi) (prodotto interno con la base diviso il prodotto interno del vettore con se stesso). Se la base è ortonormale ciò significa che gli elementi della base sono a 1 quindi non c'è denominatore.
Se ho un vettore e una base posso comunque calcolare i coefficienti della base ortogonale.
(parte mancante...)
Lezione 7 - 23 ottobre 2006
- Concetto di supporto finito del segnale
- Combinazione lineare di segnali
- Complementi sulla Delta di Dirac e dimostrazione
- Sistemi lineari ed operazioni dei sistemi lineari
Lezione 8 - 30 ottobre 2006
- Spazi vettoriali a dimensione finita con base ortogonale
- Spiegazioni più approfondite sui Sistemi Lineari
- Esercizi vari
- Prodotto di convoluzione
- Sistemi Lineari Tempo Invarianti (LTI)
- Il caso discreto (LTI a tempo discreto)
- Risposta all'impulso
Lezione 9 - 2 novembre 2006
Ricordiamo che la forma del prodotto di convoluzione è:
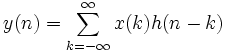 nel caso discreto
nel caso discreto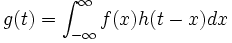 nel caso continuo
nel caso continuo
Per il prodotto di convoluzione valgono le seguenti proprietà:
- Commutativa= x(n)*h(n)= h(n)*x(n).
DIMOSTRAZIONE CASO DISCRETO: dalla definizione di prodotto di convoluzione abbiamo che 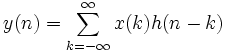 (caso discreto). Pongo l= n-k e quindi k= n-l. Perciò se k vale
(caso discreto). Pongo l= n-k e quindi k= n-l. Perciò se k vale 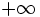 , l avrà valore
, l avrà valore 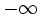 , e viceversa. Quindi abbiamo che
, e viceversa. Quindi abbiamo che 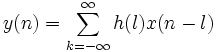 = h(n)*x(n). La variabile l è una qualunque variabile libera.
DIMOSTRAZIONE CASO CONTINUO: deve essere f(t)*h(t)=h(t)*f(t). Dato che f(t)*h(t)=
= h(n)*x(n). La variabile l è una qualunque variabile libera.
DIMOSTRAZIONE CASO CONTINUO: deve essere f(t)*h(t)=h(t)*f(t). Dato che f(t)*h(t)=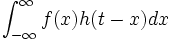 ponendo t-x= y da cui x= t-y e dx= -dy equivale a dire che se x tende a
ponendo t-x= y da cui x= t-y e dx= -dy equivale a dire che se x tende a 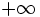 allora y tende a
allora y tende a 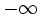 e viceversa. Quindi avremo che =)=
e viceversa. Quindi avremo che =)=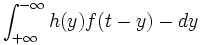 = =)=
= =)=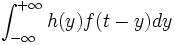 = h(t)*f(t).
= h(t)*f(t).
Il prodotto di convoluzione può essere calcolato per ogni gruppo di sequenze o segnali.
ESERCIZIO nel caso discreto (supporto finito)
Abbiamo x(n)= 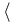 n se n=1,2,3,4, 0 altrimenti.
n se n=1,2,3,4, 0 altrimenti.
Abbiamo l'uscita h(n)= 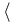 1 se n= -1,0, 1, 0 altrimenti.
Data la risposta all'impulso del sistema h(n) vogliamo calcolare la risposta nel caso in cui in ingresso ci sia x(n).
Per gli impulsi discreti abbiamo:
1 se n= -1,0, 1, 0 altrimenti.
Data la risposta all'impulso del sistema h(n) vogliamo calcolare la risposta nel caso in cui in ingresso ci sia x(n).
Per gli impulsi discreti abbiamo: 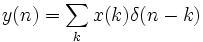 quindi x(n)=
quindi x(n)=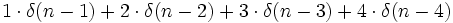 .
.
Applicandi le definizioni avremo che, dati i singoli 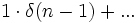 posti = x(n) avremo che, per linearità del sistema LTI che se x(n) è una somma, allora posso avere come risposta la somma delle risposte (la somma delle somme): S(x(n)+y(n))= S(x(n))+S(y(n)).
Quindi l'uscita sarà
posti = x(n) avremo che, per linearità del sistema LTI che se x(n) è una somma, allora posso avere come risposta la somma delle risposte (la somma delle somme): S(x(n)+y(n))= S(x(n))+S(y(n)).
Quindi l'uscita sarà 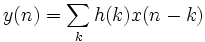 . Dato che in questo caso le uscite del sistema diverse da 0 vanno da -1 a 1 avremo che:
. Dato che in questo caso le uscite del sistema diverse da 0 vanno da -1 a 1 avremo che: 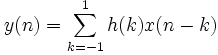 .
.
Calcoliamo...
y(0)= h(-1)x(0-(-1))+ h(0)x(0)+ h(1)x(0-1)= 1x1+ 1x0+ 1x0= 1
y(1)= h(-1)x(1-(-1))+ h(0)x(1)+ h(1)x(0)= 2+1+0= 3
y(2)= h(-1)x(3)+ h(0)x(2)+ h(1)x(1)= 6
y(3)= 9
y(4)= 7
y(5)= 4
y(6)= 0 FINITO
In pratica vado avanti fino a che non mi diventa 0.
Con due sequenze lunghe N ed M, avrò sempre una risposta di N+M-1 termini diversi da zero.
Esempi grafici del prodotto di convoluzione nel caso continuo e discreto.
Il prodotto di convoluzione, in pratica, pone le due funzioni come fossero una sopra l'altra, e, traslando una delle due, fa comparire tutto ciò che viene compreso sotto (o sopra, a seconda di come le mettete) quella che non viene traslata.
- Associativa= infatti nel caso discreto avremo che (x(n)*h1(n))*h2(n)= x(n)*(h1(n)*h2(n)). Idem nel caso continuo.
- Distributiva rispetto alla somma= x(n)*(h1(n)+h2(n))= x(n)*h1(n)+x(n)*h2(n).
- Sistema a ritardo unitario= è il più semplice sistema che ritarda un segnale, cioè lo trasla a destra sull'asse x di 1. Ad esempio da x(n)=
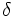 (n) diventa in uscita dal sistema h(n)=
(n) diventa in uscita dal sistema h(n)= 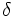 (n-1).
(n-1).
Lezione 10 - 7 novembre 2006
- Sistemi LTI causali e non causali (caso discreto e caso continuo)
- Filtro FIR
- Funzione gradino unitario U(n)
- Esercizi su filtro FIR causale
- Compito da fare su filtro FIR non causale
- Quali tra le funzioni che abbiamo visto sono LTI e quali non lo sono
- Sistema stabile (dimostrazioni)
Lezione 11 - 9 novembre 2006
- La funzione descritta nel dominio delle frequenze
- Funzione periodiche descritte come combinazione di funzioni periodiche sen e cos di diversa ampiezza
- Serie di Fourier reale
- Funzioni pari e dispari
- Spettro di ampiezza (sua derivazione)
Lezione 12 - 13 novembre 2006
- Spettro di ampiezza
- Spettro di fase
- Numeri complessi