Differenze tra le versioni di "Logica fuzzy/2007-2008"
(→Diario del corso) |
(→Diario del corso) |
||
| Riga 93: | Riga 93: | ||
* Definizione di dimostrabilità e derivabilità per modus ponens. | * Definizione di dimostrabilità e derivabilità per modus ponens. | ||
* Teorema di completezza della LPC. | * Teorema di completezza della LPC. | ||
| − | |||
| Riga 112: | Riga 111: | ||
* Definizione degli assiomi della LG e di formule deducibili (o dimostrabili). | * Definizione degli assiomi della LG e di formule deducibili (o dimostrabili). | ||
* Teorema di completezza per la LG (senza dimostrazione). | * Teorema di completezza per la LG (senza dimostrazione). | ||
| − | * Definizione di assegnamenti equivalenti su n variabili. | + | * Definizione di assegnamenti equivalenti su n variabili (che si scrive <math>\mu\equiv_n\nu</math>). |
* Lemma: dati due assegnamenti <math>\mu</math> e <math>\nu</math> equivalenti sulle prime n variabili, per ogni formula <math>\alpha \left( x_1 , \ldots , x_n \right)</math> vale: | * Lemma: dati due assegnamenti <math>\mu</math> e <math>\nu</math> equivalenti sulle prime n variabili, per ogni formula <math>\alpha \left( x_1 , \ldots , x_n \right)</math> vale: | ||
<math> | <math> | ||
| Riga 122: | Riga 121: | ||
</math> | </math> | ||
* Corollario: il problema di tautologicità della LG è decidibile. | * Corollario: il problema di tautologicità della LG è decidibile. | ||
| + | |||
| + | |||
| + | === Lezione di martedì 16/10/2007 === | ||
| + | |||
| + | * Algoritmo per la risoluzione del problema di tautologicità. | ||
| + | * Dimostrazione intuitiva del fatto che esiste sempre un assegnamento coerente con ogni catena di segni (purchè non siano tutti '='). | ||
| + | * Relazione d'ordine <math>{\leq}_n</math> tra le classi di equivalenza degli assegnamenti nella LG. | ||
| + | * Rappresentazione di <math>\mathcal{F}_n</math> (= insieme delle classi di equivalenza degli assegnamenti su n variabili nella LG) tramite diagrammi di Hasse. | ||
| + | |||
| + | |||
| + | === Lezione di venerdì 19/10/2007 === | ||
| + | |||
| + | * Definizioni di: relazione (riflessiva, simmetrica, transitiva, antisimmetrica, di equivalenza, d'ordine), insieme parzialmente ordinato (=poset), insieme totalmente ordinato (=catena), elementi inconfrontabili, sottoposet, downset, foresta, elemento minimale, minimo, albero. | ||
| + | * Lemma: per ogni n, la struttura <math>\left( \mathcal{F}_n , {\leq}_n \right)</math> è una foresta (dimostrazione lasciata per esercizio). | ||
Versione delle 11:30, 20 ott 2007
News
Appelli
Su appuntamento.
Informazioni generali
Docenti
Vincenzo Marra Stefano Aguzzoli
Corsi di laurea
Complementare per i corsi di laurea triennale in Informatica, Informatica per le Telecomunicazioni e Comunicazione Digitale e per il corso di laurea magistrale in Informatica.
Programma
- Prima Parte (Marra)
Introduzione alla logica fuzzy e alle sue applicazioni. Logica proposizionale booleana. Norme triangolari e relative logiche fuzzy. Introduzione alla logica di Gödel. Semantica della logica di Gödel. Completezza della logica di Gödel. Una semantica alternativa per la logica di Gödel. Logica di Gödel e logica booleana a confronto.
- Seconda Parte (Aguzzoli)
Introduzione alla logica di Łukasiewicz. Logica di Łukasiewicz e logica di Gödel a confronto. Semantica della logica di Łukasiewicz: le MV-algebre di Chang. Completezza della logica di Łukasiewicz. Teorema di rappresentazione di McNaughton. Complessità computazionale dei problemi di soddisfacibilità e tautologicità della logica di Łukasiewicz. Un approccio generale alle gerarchie di logiche fuzzy: cenni a BL e MTL.
Seminari
- Nell'anno accademico 2007-2008 si prevedono i seminari seguenti:
Paolo Amato, ST Microelectronics. Titolo da stabilirsi. Data da stabilirsi. Matteo Bianchi, Università di Milano. Estensioni predicative delle logiche fuzzy. Data da stabilirsi. Simone Bova, Università di Siena. Introduzione alla Basic Fuzzy Logic di Hájek. Data da stabilirsi.
Modalità d'esame
L'esame consiste in un colloquio con i docenti sul programma del corso.
Gli studenti che ne facciano richiesta possono anche concordare con i docenti la redazione di una tesina o lo sviluppo di un progetto in sostituzione di parti del programma.
Alcuni esempi di tesine: relazione su un articolo di ricerca; rassegna della letteratura scientifica su un argomento di ricerca.
Alcuni esempi di progetti: implementazione (in C, Java, Prolog, etc.) di algoritmi inerenti al programma del corso; sviluppo di software di supporto alla ricerca nel campo della logica fuzzy.
Prerequisiti al corso
Nessuno.
Orari e luogo delle lezioni
- Martedì 13.30-15.30 auletta 5 (Comelico)
- Venerdì 13.30-15.30 auletta 5 (Comelico)
Orario di ricevimento studenti
- Marra: su appuntamento.
- Aguzzoli: mercoledì dalle 15.00 alle 16.00 o su appuntamento, stanza S204 via Comelico 39.
Materiale didattico
Non ci sono testi che coprano interamente gli argomenti trattati, ma il contenuto delle lezioni è sufficiente per sostenere l'esame.
Testi ausiliari consigliati
R. L. O. Cignoli, I. M. L. D'Ottaviano e D. Mundici, Algebraic Foundations of Many-Valued Reasoning, Kluwer, 1999. P. Hájek, Metamathematics of Fuzzy Logic, Kluwer, 1998. S. Gottwald, A Treatise on Many-Valued Logics, King's College Publications, Research Studies Press, 2001.
Dispense
Durante le lezioni verrà distribuita una versione preliminare delle dispense del corso.
Diario del corso
Lezione di martedì 2/10/2007
- Definizione di logica fuzzy in senso stretto e in senso ampio.
- Concetti di funzione di appartenenza e di insiemi fuzzy.
- Richiamo di logica proposizionale classica: definizioni di proposizione atomica, proposizione composta, alfabeto, stringa, formula.
Lezione di venerdì 5/10/2007
Semantica della logica proposizionale classica
- Assegnamento alle variabili e assegnamento alle formule.
- Definizioni di tautologia, contraddizione e formula soddisfacibile.
- Esempi di tautologie: prelinearità, principio del terzo escluso, ex falso quodlibet, leggi di de Morgan.
Teoria della dimostrazione (sintassi)
- Assiomi della LPC.
- Definizione di dimostrabilità e derivabilità per modus ponens.
- Teorema di completezza della LPC.
Lezione di martedì 9/10/2007
Logica di Gödel
- Definizione di assegnamento alle variabili e alle formule nella LG (e variante di Zadeh).
- Analisi di alcune tautologie della LC che cadono nella LG (legge della doppia negazione, principio del terzo escluso) o restano tautologie (ex falso quodlibet, prelinearità).
- Inclusione stretta dell'insieme delle tautologie della LG nell'insieme delle tautologie della LC.
- Introduzione del problema di tautologicità nella LG.
- Lemma: l'insieme dei possibili valori di verità di una formula è composto da 1, 0 e i valori di verità delle variabili coinvolte nella formula.
Oggi sono state distribuite le fotocopie del primo capitolo delle dispense.
Lezione di venerdì 12/10/2007
- Definizione degli assiomi della LG e di formule deducibili (o dimostrabili).
- Teorema di completezza per la LG (senza dimostrazione).
- Definizione di assegnamenti equivalenti su n variabili (che si scrive
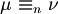 ).
). - Lemma: dati due assegnamenti
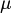 e
e 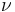 equivalenti sulle prime n variabili, per ogni formula
equivalenti sulle prime n variabili, per ogni formula 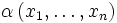 vale:
vale:
- Corollario: il problema di tautologicità della LG è decidibile.
Lezione di martedì 16/10/2007
- Algoritmo per la risoluzione del problema di tautologicità.
- Dimostrazione intuitiva del fatto che esiste sempre un assegnamento coerente con ogni catena di segni (purchè non siano tutti '=').
- Relazione d'ordine
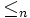 tra le classi di equivalenza degli assegnamenti nella LG.
tra le classi di equivalenza degli assegnamenti nella LG. - Rappresentazione di
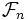 (= insieme delle classi di equivalenza degli assegnamenti su n variabili nella LG) tramite diagrammi di Hasse.
(= insieme delle classi di equivalenza degli assegnamenti su n variabili nella LG) tramite diagrammi di Hasse.
Lezione di venerdì 19/10/2007
- Definizioni di: relazione (riflessiva, simmetrica, transitiva, antisimmetrica, di equivalenza, d'ordine), insieme parzialmente ordinato (=poset), insieme totalmente ordinato (=catena), elementi inconfrontabili, sottoposet, downset, foresta, elemento minimale, minimo, albero.
- Lemma: per ogni n, la struttura
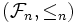 è una foresta (dimostrazione lasciata per esercizio).
è una foresta (dimostrazione lasciata per esercizio).