Differenze tra le versioni di "Informazione e trasmissione"
m (→Lezione del giorno 5/4/2006) |
(Lezione del giorno 7/4/2006) |
||
| Riga 123: | Riga 123: | ||
Venerdì 14, Mercoledì 19 e Venerdì 21 Aprile non si terrà lezione. | Venerdì 14, Mercoledì 19 e Venerdì 21 Aprile non si terrà lezione. | ||
Il corso si concluderà probabilmente il giorno 26 Maggio. | Il corso si concluderà probabilmente il giorno 26 Maggio. | ||
| + | |||
| + | === Lezione del giorno 7/4/2006 === | ||
| + | * esercizi di calcolo delle entropie spiegate durante la lezione precedente | ||
| + | * teorema (con dimostrazione) | ||
| + | ** H(S,R) = H(S) + H(R|S) | ||
| + | ** H(S,R) = H(R) + H(S|R) | ||
| + | ** H(S) - H(S|R) = H(R) - H(R|S) | ||
Versione delle 15:16, 7 apr 2006
Indice
- 1 News
- 2 Informazioni generali
- 3 Informazioni specifiche
- 4 Materiale didattico
- 5 Diario del corso
- 5.1 Lezione del giorno 8/3/2006
- 5.2 Lezione del giorno 10/3/2006
- 5.3 Lezione del giorno 15/3/2006
- 5.4 Lezione del giorno 17/3/2006
- 5.5 Lezione del giorno 22/3/2006
- 5.6 Lezione del giorno 24/3/2006
- 5.7 Lezione del giorno 29/3/2006
- 5.8 Lezione del giorno 31/3/2006
- 5.9 Lezione del giorno 5/4/2006
- 5.10 Lezione del giorno 7/4/2006
News
http://www.dico.unimi.it/avvisi.php?z=0;pagina=avvisistudenti
Informazioni generali
Docenti
Anastasia Pagnoni
Corsi di laurea
Corso di laurea magistrale in Informatica
Modalità d'esame
Esame orale * sugli argomenti trattati a lezione, per i frequentanti * sugli argomenti indicati nel programma d'esame disponibile sul sito del corso
Orari e luogo delle lezioni
* Mercoledì 11.45 - 13.15 Aula Alfa * Venerdì 10.45 - 12.15 Aula Alfa
Orario di ricevimento studenti
Indicato qui
Informazioni specifiche
Siti del corso
http://homes.dico.unimi.it/pagnoni/pagina%20Informazione%20e%20Trasmissione.htm
Forum del corso, e affini
Forum DSY del corso
Materiale didattico
Programma del corso
Disponibile qui (formato DOC)
Slides
Messe a disposizione dal docente solo agli studenti frequentanti
Testi
Francesco Fabris, Teoria dell’informazione, codici, cifrari, Bollati-Boringhieri, 2001 Thomas M. Cover, Joy A. Thomas, Elements of Information Theory, John Wiley & Sons, New York, 1991
Diario del corso
Lezione del giorno 8/3/2006
- introduzione generale al corso
- contributi storici di Morse, Hartley e Wiener alla trasmissione dell'informazione
- Shannon
- modello
- primo teorema
- teorema fondamentale
- sorgente
- sorgente uniforme
- sorgente deterministica
- Interpretazione I(p)
- la funzione logaritmica considerata da Shannon come funzione I(p)
- teorema di unicità della soluzione di Cauchy
Lezione del giorno 10/3/2006
- ripasso dei logaritmi e delle loro principali proprietà
- funzione entropia
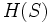
- definizioni
- esempi di calcolo
- disuguaglianza di Gibbs
- valore massimo della funzione entropia
Lezione del giorno 15/3/2006
- codifica
- sorgente
- canale
- introduzione ai codici
- a lunghezza variabile
- a blocco
- istantanei
- compatti
- binari
- a virgola
- alberi rappresentativi dei codici
- teorema di Kraft (solo enunciato)
Lezione del giorno 17/3/2006
- algoritmo di Sardinas-Patterson
- enunciato
- dimostrazione
- codice efficiente
- codice ottimale
- teorema di Kraft (dimostrazione)
- teorema di McMillan (enunciato)
Lezione del giorno 22/3/2006
- teorema di McMillan (dimostrazione)
- lunghezza media di un codice sorgente
- codice ottimale
- codice e algoritmo di Huffman
Lezione del giorno 24/3/2006
- esercizi sui codici di Huffman
- enunciato e dimostrazione del teorema del lower bound della lunghezza media di un codice istantaneo ed efficiente
Lezione del giorno 29/3/2006
- codice di Shannon-Fano
- estensione
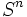 di una sorgente
di una sorgente - enunciato del teorema
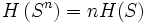
Lezione del giorno 31/3/2006
- dimostrazione del teorema
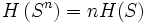
- canale
- matrice di canale
- introduzione ai codici a riconoscimento e a correzione d'errore
Lezione del giorno 5/4/2006
- entropia
- della sorgente
- del ricevente
- congiunta (della sorgente e del ricevente)
- della sorgente, posto il ricevente
- del ricevente, posta la sorgente
Venerdì 14, Mercoledì 19 e Venerdì 21 Aprile non si terrà lezione. Il corso si concluderà probabilmente il giorno 26 Maggio.
Lezione del giorno 7/4/2006
- esercizi di calcolo delle entropie spiegate durante la lezione precedente
- teorema (con dimostrazione)
- H(S,R) = H(S) + H(R|S)
- H(S,R) = H(R) + H(S|R)
- H(S) - H(S|R) = H(R) - H(R|S)