Differenze tra le versioni di "Matematica discreta/Esami/2002-xx-xx"

Versione delle 15:40, 17 feb 2006

Compitino prof. Bonzini del 2002

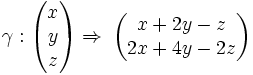(funzione da 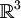a )
1. $\gamma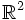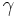$ è omomorfismo di spazi vettoriali
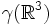2. $\gamma ({\mathbb {R}}^{3})$ è la retta di 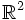${\mathbb {R}}^{2}$ generata da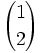 ${1 \choose 2}$
3. ogni classe della 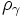$\rho _{\gamma }$ è un piano parallelo a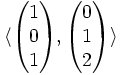 $\langle {\begin{pmatrix}1\\0\\1\end{pmatrix}},{\begin{pmatrix}0\\1\\2\end{pmatrix}}\rangle$
4. il piano 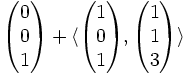${\begin{pmatrix}0\\0\\1\end{pmatrix}}+\langle {\begin{pmatrix}1\\0\\1\end{pmatrix}},{\begin{pmatrix}1\\1\\3\end{pmatrix}}\rangle$ è una classe della relazione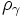 $\rho _{\gamma }$
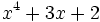quoziente e resto in $({\mathbb {Z}}_{7}[x],+,\cdot )$ di $x^{4}+3x+2$ con $4x^{2}+1$

@@ Riga 1: / Riga 1: @@
 Compitino prof. [[Bonzini]] del '''2002'''
-#<math> \gamma : \begin{pmatrix} x \\ y \\ z \end{pmatrix} \Rightarrow \; \begin{pmatrix} x+2y-z\\ 2x+4y-2z \end{pmatrix}</math> (funzione da <math> \mathbb{R}\ ^3 </math> a <math> \mathbb{R}\ ^2 </math>)
+#<math> \gamma : \begin{pmatrix} x \\ y \\ z \end{pmatrix} \Rightarrow \; \begin{pmatrix} x+2y-z\\ 2x+4y-2z \end{pmatrix}</math> (funzione da <math> \mathbb{R}^3 </math> a <math> \mathbb{R}^2 </math>)
 ## '''<math> \gamma </math>''' è omomorfismo di spazi vettoriali
-## <math> \gamma ( \mathbb{R}\ ^3 ) </math> è la retta di <math> \mathbb{R}\ ^2 </math> generata da <math> {1 \choose 2} </math>
+## <math> \gamma ( \mathbb{R}^3 ) </math> è la retta di <math> \mathbb{R}^2 </math> generata da <math> {1 \choose 2} </math>
 ## ogni classe della '''<math> \rho_\gamma </math>''' è un piano parallelo a <math> \langle \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} \rangle </math>
 ## il piano <math> \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \langle \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix} \rangle </math> è una classe della relazione '''<math> \rho_\gamma </math>'''