- Questa pagina è stata modificata per l'ultima volta il 7 gen 2008 alle 17:57.
- Contenuto disponibile sotto GNU Free Documentation License.
Compitino prof. Bonzini del 2002
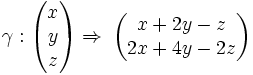 (funzione da
(funzione da 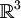 a
a 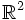 )
)
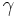 è omomorfismo di spazi vettoriali
è omomorfismo di spazi vettoriali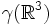 è la retta di
è la retta di 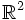 generata da
generata da 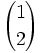
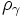 è un piano parallelo a
è un piano parallelo a 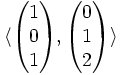
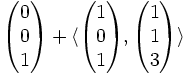 è una classe della relazione
è una classe della relazione 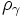
![({\mathbb {Z}}_{7}[x],+,\cdot )](/images/math/9/2/8/9282860f41f9dcb89143fcb348b5239f.png) di
di 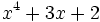 con
con