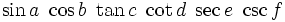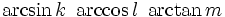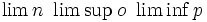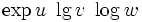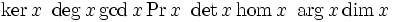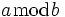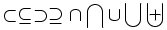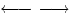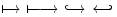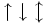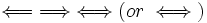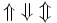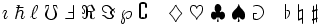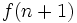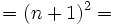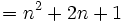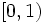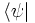Aiuto:Formule matematiche TeX

Da WikiDsy.
Versione del 20 feb 2009 alle 12:06 di Walter (discussione | contributi) (Riportata alla revisione precedente da 87.2.170.3)
 Questa pagina è la traduzione della pagina inglese meta:Help:Formula tratta da Wikipedia.
 Verrà aggiornata di tanto in tanto, ma la pagina inglese resta la guida di riferimento ufficiale.

Da febbraio 2006 è stato aggiunta la possibilità di usare su WikiDsy dei comandi TeX per formule matematiche. Tali stringhe nel caso di espressioni semplici generano del semplice markup HTML, nel caso di espressioni elaborate generano immagini PNG di maggiore evidenza che si differenziano dalle parti verbali. Se si vuole dare evidenza anche ad espressioni semplici, basta renderle elaborate aggiungendo richieste di spaziatura (v.o.). Nel futuro, col miglioramento dei browser, si apriranno possibilità di generare markup HTML (o XHTML) più sofisticato e di richiedere anche inserti MathML (e di controllare grafici con richieste in SVG).

Ogni markup matematico deve rientrare all'interno dei due tag <math> ... </math>.
Le interruzioni fisiche di linea all'interno di questi tag non vengono tradotte. Si possono invece richiedere interruzioni di linea e altri posizionamenti con richieste apposite (ad esempio, un'interruzione di linea dopo ogni termine o riga di una matrice).

Per problemi con gli stili che riguardino la composizione di contenuto matematico si guardi: WikiProject Mathematics (in inglese). In particolare, si prega di evitare l'uso di formule in una riga di testo normale dato che le formule non hanno un allineamento coerente con il resto e il loro font ha una misura superiore.

MediaWiki e TeX

MediaWiki usa un sottoinsieme dei markup di TeX (incluse qualche estensione di LaTeX e AMSLaTeX) per la formattazione di formule matematiche. Può essere generata un'immagine PNG oppure una semplice stringa di HTML. Quello che viene mostrato all'utente dipende dalle sue preferenze e dalla complessità dell'espressione. In futuro, come molti browser sono già in grado di fare, sarà possibile sfruttare, oltre all'HTML il linguaggio di markup MathML.

Più precisamente MediaWiki filtra il markup attraverso Texvc, che converte i comandi in TeX per poi darli in pasto al motore di rendering, così che solo una piccola parte del linguaggio TeX è supportata. Per maggiori dettagli vedi di seguito.

Sintassi

I comandi di TeX vanno racchiusi nei markup <math> ... </math>. La barra degli strumenti per la modifica contiene un pulsante apposito per questa operazione, vedi Modificare la barra degli strumenti.

TeX tratta gli spazi bianchi e i ritorno-a-capo in modo molto simile all'HTML, cioè vengono ignorati, ma vedremo in seguito come aggirare questo problema (anche se non si tratta di un vero e proprio problema).

Funzioni, simboli, caratteri speciali

Caratteristica Sintassi Come appare
Accenti \acute{a} \quad \grave{a} \quad \breve{a} \quad \check{a} \quad \tilde{a} {\acute {a}}\quad {\grave {a}}\quad {\breve {a}}\quad {\check {a}}\quad {\tilde {a}}\!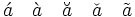
Funzioni elementari (metodo corretto) \sin x + \ln y +\operatorname{sgn} z

\sin a \ \cos b \ \tan c \ \cot d \ \sec e \ \csc f
\sinh g \ \cosh h \ \tanh i \ \coth j
\arcsin k \ \arccos l \ \arctan m
\lim n \ \limsup o \ \liminf p
\min q \ \max r \ \inf s \ \sup t
\exp u \ \lg v \ \log w
\ker x \ \deg x \gcd x \Pr x \ \det x \hom x \ \arg x \dim x

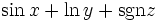
\sin x+\ln y+\operatorname {sgn}z

\sin a\ \cos b\ \tan c\ \cot d\ \sec e\ \csc f\!
\sinh g\ \cosh h\ \tanh i\ \coth j\!
\arcsin k\ \arccos l\ \arctan m\!
\lim n\ \limsup o\ \liminf p\!
\min q\ \max r\ \inf s\ \sup t\!
\exp u\ \lg v\ \log w\!
\ker x\ \deg x\gcd x\Pr x\ \det x\hom x\ \arg x\dim x\!

Funzioni elementari (metodo non corretto) sin x + ln y + sgn z sinx+lny+sgnz\,\!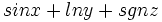
Aritmetica dell'orologio s_k \equiv 0 \pmod{m}

a \bmod b

s_{k}\equiv 0{\pmod {m}}\!

a{\bmod b}\,\!

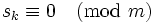
Derivate \nabla \; \partial x \; dx \; \dot x \; \ddot y \nabla \;\partial x\;dx\;{\dot x}\;{\ddot y}\!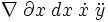
Insiemi \forall \; \exists \; \empty \; \emptyset \; \varnothing \in \ni \not\in \notin

\subset \subseteq \supset \supseteq \cap \bigcap \cup \bigcup \biguplus

\forall \;\exists \;\emptyset \;\emptyset \;\varnothing \in \ni \not \in \notin \!

\subset \subseteq \supset \supseteq \cap \bigcap \cup \bigcup \biguplus \!

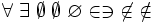
\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup \sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup \!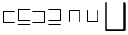
Logica p \land \wedge \; \bigwedge \; \bar{q} \to p \; \lor \vee \; \bigvee \; \lnot \; \neg q \; \setminus \; \smallsetminus p\land \wedge \;\bigwedge \;{\bar {q}}\to p\lor \vee \;\bigvee \;\lnot \;\neg q\;\setminus \;\smallsetminus \!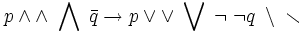
Radicali \sqrt{2}\approx 1.4 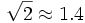{\sqrt {2}}\approx 1.4\!
\sqrt[n]{x} {\sqrt[ {n}]{x}}\!
Simboli relazionali \sim \; \approx \; \simeq \; \cong \; \le \; < \; \ll \; \gg \; \ge \; > \; \equiv \; \not\equiv \; \ne \; \propto \; \pm \; \mp 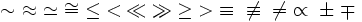\sim \;\approx \;\simeq \;\cong \;\leq \;<\;\ll \;\gg \;\geq \;>\;\equiv \;\not \equiv \;\neq \;\propto \;\pm \;\mp \!
Simboli geometrici \Diamond \; \Box \; \triangle \; \angle \; \perp \; \mid \; \nmid \; \| \; 45^\circ \Diamond \;\Box \;\triangle \;\angle \;\perp \;\mid \;\nmid \;\|\;45^{\circ }\!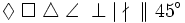
Frecce \leftarrow \; \gets \; \rightarrow \; \to \; \leftrightarrow

\longleftarrow \; \longrightarrow
\mapsto \; \longmapsto \; \hookrightarrow \; \hookleftarrow
\nearrow \; \searrow \; \swarrow \; \nwarrow
\uparrow \; \downarrow \; \updownarrow

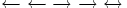
\leftarrow \;\gets \;\rightarrow \;\to \;\leftrightarrow \!

\longleftarrow \;\longrightarrow \!
\mapsto \;\longmapsto \;\hookrightarrow \;\hookleftarrow \!
\nearrow \;\searrow \;\swarrow \;\nwarrow \!
\uparrow \;\downarrow \;\updownarrow \!

\rightharpoonup \; \rightharpoondown \; \leftharpoonup \; \leftharpoondown \; \upharpoonleft \; \upharpoonright \; \downharpoonleft \; \downharpoonright \rightharpoonup \;\rightharpoondown \;\leftharpoonup \;\leftharpoondown \;\upharpoonleft \;\upharpoonright \;\downharpoonleft \;\downharpoonright \!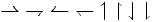
\Leftarrow \; \Rightarrow \; \Leftrightarrow

\Longleftarrow \; \Longrightarrow \; \Longleftrightarrow (or \iff)
\Uparrow \; \Downarrow \; \Updownarrow

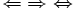
\Leftarrow \;\Rightarrow \;\Leftrightarrow \!

\Longleftarrow \;\Longrightarrow \;\Longleftrightarrow (or\iff )\!
\Uparrow \;\Downarrow \;\Updownarrow \!

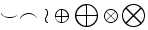
Simboli speciali \eth \; \S \; \P \; \% \; \dagger \; \ddagger \; \star \; * \; \ldots

\smile \frown \wr \oplus \bigoplus \otimes \bigotimes
\times \cdot \circ \bullet \bigodot \triangleleft \triangleright \infty \bot \top \vdash \vDash \Vdash \models \lVert \rVert
\imath \; \hbar \; \ell \; \mho \; \Finv \; \Re \; \Im \; \wp \; \complement \quad \diamondsuit \; \heartsuit \; \clubsuit \; \spadesuit \; \Game \quad \flat \; \natural \; \sharp

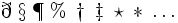
\eth \;\S \;\P \;\%\;\dagger \;\ddagger \;\star \;*\;\ldots \!

\smile \frown \wr \oplus \bigoplus \otimes \bigotimes \!
\times \cdot \circ \bullet \bigodot \triangleleft \triangleright \infty \bot \top \vdash \vDash \Vdash \models \lVert \rVert \!
\imath \;\hbar \;\ell \;\mho \;\Finv \;\Re \;\Im \;\wp \;\complement \quad \diamondsuit \;\heartsuit \;\clubsuit \;\spadesuit \;\Game \quad \flat \;\natural \;\sharp \!

Le lettere minuscole con \mathcal consentono caratteri extra \mathcal {45abcdenpqs} {\mathcal {45abcdenpqs}}\!

Apici, pedici, integrali

Caratteristica Sintassi Come appare
    HTML PNG
Apice a^2 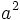a^{2} a^{2}\!
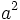
Pedice a_2 a_{2} a_{2}\!
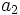
Raggruppamento a^{2+2} 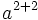a^{{2+2}} a^{{2+2}}\!
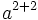
a_{i,j} a_{{i,j}} a_{{i,j}}\!
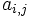
Combinazione di apici e pedici x_2^3 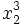x_{2}^{3} x_{2}^{3}\!
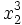
Derivate (forzato in PNG) x', y, f', f  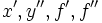 x',y'',f',f''\!
Derivate (il corsivo sovrappone gli apici) x', y, f', f 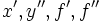x',y'',f',f'' x',y'',f',f''\!
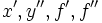
Derivate (errato in HTML) x^\prime, y^{\prime\prime} x^{\prime },y^{{\prime \prime }} x^{\prime },y^{{\prime \prime }}\!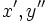
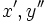
Derivate (errato in PNG) x\prime, y{\prime\prime} x\prime ,y{\prime \prime } x\prime ,y{\prime \prime }\!
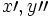
Sottolineato, sopralineato, vettori \hat a \ \bar b \ \vec c \ \overrightarrow{a b} \ \overleftarrow{c d} \ \widehat{d e f} \ \overline{g h i} \ \underline{j k l} {\hat a}\ {\bar b}\ {\vec c}\ \overrightarrow {ab}\ \overleftarrow {cd}\ \widehat {def}\ \overline {ghi}\ \underline {jkl}\!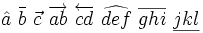
Parentesi sopra \begin{matrix} 5050 \\ \overbrace{ 1+2+\cdots+100 } \end{matrix} {\begin{matrix}5050\\\overbrace {1+2+\cdots +100}\end{matrix}}\!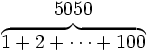
Parentesi sotto \begin{matrix} \underbrace{ a+b+\cdots+z } \\ 26 \end{matrix} {\begin{matrix}\underbrace {a+b+\cdots +z}\\26\end{matrix}}\!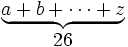
Sommatoria \sum_{k=1}^N k^2 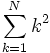\sum _{{k=1}}^{N}k^{2}
Sommatoria (forzando il \textstyle) \begin{matrix} \sum_{k=1}^N k^2 \end{matrix} {\begin{matrix}\sum _{{k=1}}^{N}k^{2}\end{matrix}}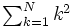
Produttoria \prod_{i=1}^N x_i \prod _{{i=1}}^{N}x_{i}
Produttoria (forzando il \textstyle) \begin{matrix} \prod_{i=1}^N x_i \end{matrix} {\begin{matrix}\prod _{{i=1}}^{N}x_{i}\end{matrix}}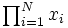
Coproduttoria \coprod_{i=1}^N x_i 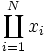\coprod _{{i=1}}^{N}x_{i}
Coproduttoria (forzando il \textstyle) \begin{matrix} \coprod_{i=1}^N x_i \end{matrix} {\begin{matrix}\coprod _{{i=1}}^{N}x_{i}\end{matrix}}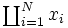
Limite \lim_{n \to \infty}x_n 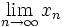\lim _{{n\to \infty }}x_{n}
Limite (forzando il \textstyle) \begin{matrix} \lim_{n \to \infty}x_n \end{matrix} {\begin{matrix}\lim _{{n\to \infty }}x_{n}\end{matrix}}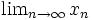
Integrale \int_{-N}^{N} e^x\, dx 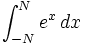\int _{{-N}}^{{N}}e^{x}\,dx
Integrale (forzando il \textstyle) \begin{matrix} \int_{-N}^{N} e^x\, dx \end{matrix} {\begin{matrix}\int _{{-N}}^{{N}}e^{x}\,dx\end{matrix}}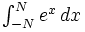
Integrale doppio \iint_{D}^{W} \, dx\,dy \iint _{{D}}^{{W}}\,dx\,dy
Integrale triplo \iiint_{E}^{V} \, dx\,dy\,dz 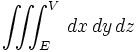\iiint _{{E}}^{{V}}\,dx\,dy\,dz
Integrale quadruplo \iiiint_{F}^{U} \, dx\,dy\,dz\,dt \iiiint _{{F}}^{{U}}\,dx\,dy\,dz\,dt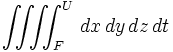
Integrale curvilineo \oint_{C} x^3\, dx + 4y^2\, dy 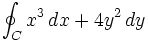\oint _{{C}}x^{3}\,dx+4y^{2}\,dy
Intersezioni \bigcap_1^{n} p 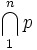\bigcap _{1}^{{n}}p
Unioni \bigcup_1^{k} p \bigcup _{1}^{{k}}p

Frazioni, matrici, multi-linea

Caratteristica Sintassi Come appare
Frazioni \frac{2}{4} or {2 \over 4} 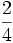{\frac {2}{4}}\!
Coefficienti binomiali \binom{n}{k} or {n \choose k} 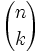{n \choose k}
Matrici \begin{matrix} x & y \\ z & v \end{matrix} 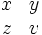{\begin{matrix}x&y\\z&v\end{matrix}}\!
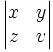
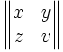
\begin{vmatrix} x & y \\ z & v \end{vmatrix} {\begin{vmatrix}x&y\\z&v\end{vmatrix}}\!
\begin{Vmatrix} x & y \\ z & v \end{Vmatrix} {\begin{Vmatrix}x&y\\z&v\end{Vmatrix}}\!
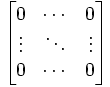
\begin{bmatrix} 0 & \cdots & 0 \\ \vdots &

\ddots & \vdots \\ 0 & \cdots &
0\end{bmatrix}\begin{vmatrix} x & y \\ z & v \end{vmatrix}

{\begin{bmatrix}0&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &0\end{bmatrix}}
\begin{Bmatrix} x & y \\ z & v \end{Bmatrix} {\begin{Bmatrix}x&y\\z&v\end{Bmatrix}}\,\!
\begin{Bmatrix} x & y \\ z & v \end{Bmatrix} 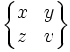{\begin{Bmatrix}x&y\\z&v\end{Bmatrix}}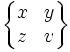
Distinzione di casi f(n)=\left\{\begin{matrix} n/2, & \mbox{se }n\mbox{ pari} \\ 3n+1, & \mbox{se }n\mbox{ dispari}

\end{matrix}\right.

f(n)=\left\{{\begin{matrix}n/2,&{\mbox{se }}n{\mbox{ pari}}\\3n+1,&{\mbox{se }}n{\mbox{ dispari}}\end{matrix}}\right.
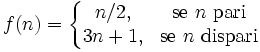
Equazioni su più righe \begin{matrix}f(n+1)&=& (n+1)^2 &= \\ \ & =& n^2 + 2n + 1 \end{matrix} {\begin{matrix}f(n+1)&=&(n+1)^{2}&=\\\ &=&n^{2}+2n+1\end{matrix}}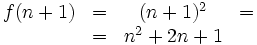
Equazioni su più righe (alternativa usando le tabelle) 

{|
|-
|<math>f(n+1)</math>
|<math>=(n+1)^2=</math>
|-
|
|<math>=n^2 + 2n + 1</math>
|}
f(n+1)\! =(n+1)^{2}=\!
=n^{2}+2n+1\!

Font

Caratteristica Sintassi Come appare
Lettere greche maiuscole \Alpha \Beta \Gamma \Delta \Epsilon \Zeta \Eta \Theta \Iota \Kappa \Lambda \Mu \Nu \Xi \Pi \Rho \Sigma \Tau \Upsilon \Phi \Chi \Psi \Omega 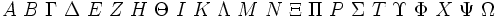\mathrm{A} \ \mathrm{B} \ \Gamma \ \Delta \ \mathrm{E} \ \mathrm{Z} \ \mathrm{H} \ \Theta \ \mathrm{I} \ \mathrm{K} \ \Lambda \ \mathrm{M} \ \mathrm{N} \ \Xi \ \Pi \ \mathrm{P} \ \Sigma \ \mathrm{T} \ \Upsilon \ \Phi \ \mathrm{X} \ \Psi \ \Omega \!
Lettere greche minuscole \alpha \beta \gamma \delta \epsilon \zeta \eta \theta \iota \kappa \lambda \mu \nu \xi \pi \rho \sigma \tau \upsilon \phi \chi \psi \omega \alpha \ \beta \ \gamma \ \delta \ \epsilon \ \zeta \ \eta \ \theta \ \iota \ \kappa \ \lambda \ \mu \ \nu \ \xi \ \pi \ \rho \ \sigma \ \tau \ \upsilon \ \phi \ \chi \ \psi \ \omega \!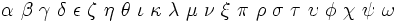
Altre lettere greche \varepsilon \digamma \vartheta \varkappa \varpi \varrho \varsigma \varphi \varepsilon \ \digamma \ \vartheta \ \varkappa \ \varpi \ \varrho \ \varsigma \ \varphi \!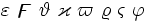
Grassetto lavagna \mathbb{N}\ \mathbb{Z}\ \mathbb{Q}\ \mathbb{R}\ \mathbb{C} {\mathbb {N}}\ {\mathbb {Z}}\ {\mathbb {Q}}\ {\mathbb {R}}\ {\mathbb {C}}\!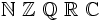
Grassetto (per vettori) \mathbf{x}\cdot\mathbf{y} = 0 {\mathbf {x}}\cdot {\mathbf {y}}=0\!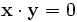
Grassetto per lettere greche \boldsymbol{\alpha} + \boldsymbol{\beta} + \boldsymbol{\gamma} {\boldsymbol {\alpha }}+{\boldsymbol {\beta }}+{\boldsymbol {\gamma }}\!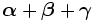
Corsivo \mathit{ABCDE abcde 1234} {\mathit {ABCDEabcde1234}}\!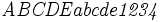
Font Roman \mathrm{ABCDE abcde 1234} {\mathrm {ABCDEabcde1234}}\!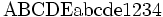
Font Fraktur \mathfrak{ABCDE abcde 1234} {\mathfrak {ABCDEabcde1234}}\!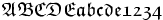
Calligrafico \mathcal{ABCDE abcde 1234} {\mathcal {ABCDEabcde1234}}\!
Lettere ebraiche \aleph \beth \gimel \daleth \aleph \ \beth \ \gimel \ \daleth \!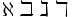
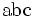
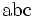
Caratteri non corsivi \mbox{abc} {\mbox{abc}} {\mbox{abc}}\!
Misto corsivo (cattivo esempio) \mbox{se} n \mbox{pari} {\mbox{se}}n{\mbox{pari}} {\mbox{se}}n{\mbox{pari}}\,\!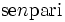
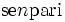
Misto corsivo (buon esempio) \mbox{se } n \mbox{ pari} {\mbox{se }}n{\mbox{ pari}} {\mbox{se }}n{\mbox{ pari}}\,\!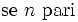

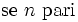
Le parentesi nelle espressioni estese

Caratteristica Sintassi Traduzione
Da evitare ( \frac{1}{2} ) 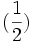({\frac {1}{2}})
Preferibile \left( \frac{1}{2} \right) \left({\frac {1}{2}}\right)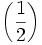

Si possono usare vari delimitatori con \left e \right:

Caratteristica Sintassi Come appare
Parentesi tonde \left ( A \right ) 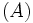\left(A\right)
Parentesi quadre \left [ A \right ] \left[A\right]
Parentesi graffe \left \{ A \right \} 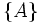\left\{A\right\}
Parentesi angolari \left \langle A \right \rangle \left\langle A\right\rangle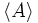
Barre semplici e doppie \left | A \right | and \left \| B \right \| \left|A\right|and\left\|B\right\|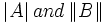

I delimitatori possono essere combinati,
facendoli corrispondere con \left e \right

\left [ 0,1 \right )
\left \langle \psi \right |

\left[0,1\right)
\left\langle \psi \right|

Usare \left. and \right. se si vuole
omettere un delimitatore:		 \left . \frac{A}{B} \right \} \to X \left.{\frac {A}{B}}\right\}\to X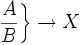

Spaziatura

Si rammenta che TeX tratta la spaziatura in modo per lo più automatico, ma a volte può essere necessario controllarla direttamente.

Caratteristica Sintassi Traduzione
Doppia spaziatura quad a \qquad b a\qquad b
Spaziatura quad a \quad b a\quad b
Spaziatura del testo a\ b 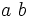a\ b
Spaziatura grande a\;b 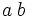a\;b
Spaziatura media a\>b [non supportata]
Spaziatura piccola a\,b 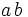a\,b
Nessuna spaziatura ab 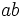ab\,
Spaziatura negativa a\!b 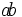a\!b

Allineamento col testo normale

Di default nello stile CSS abbiamo: 

img.tex { vertical-align: middle; }

per questo un'espressione come 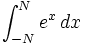\int _{{-N}}^{{N}}e^{x}\,dx appare così.

Se dovete assolutamente allineare in altro modo usate <div style="vertical-align:-100%;display:inline;"><math>...</math></div> e giocate con il valore di vertical-align finchè non raggiungete il risultato desiderato. Comunque molto spesso il rendering cambia da browser a browser, non preoccupatevi se a casa vostra vedete una cosa e dal vostro amico un'altra.

Forzare il rendering PNG

Se necessario, è possibile forzare che una formula venga resa in PNG, senza influenzare l'aspetto della formula, aggiungendo \,\! (spazio ridotto e spazio negativo, che si elidono) ovunque all'interno del tag math (possibilmente al termine).

Ciò potrebbe essere utile per mantenere il rendering delle formule uniforme, per esempio, o per correggere una formula che viene resa in modo sbagliato con l'HTML (x derivato, oppure a^{2+2}), o per dimostrare come viene reso qualcosa normalmente visualizzato come HTML (come nell'esempio precedente). Per esempio:

Sintassi Come appare
a^{2+2} a^{{2+2}}
a^{2+2} 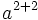\,\! a^{{2+2}}\,\!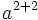
\int_{-N}^{N} e^x\, dx 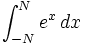\int _{{-N}}^{{N}}e^{x}\,dx
\int_{-N}^{N} e^x\, dx \,\! \int _{{-N}}^{{N}}e^{x}\,dx\,\!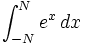

È stato testato con la maggior parte delle formule di questa pagina, e sembra funzionare perfettamente.

Sarebbe opportuno inserire un commento nel codice HTML per evitare che qualcuno "corregga" la formula rimuovendolo:

<!-- Il tag \,\! serve per rendere la formula come PNG invece che come HTML. Si prega di non rimuoverlo.-->

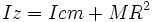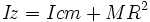È possibile come ulteriore opzione aggiungere \emph prima di ogni formula all'interno del tag <math> per avere il rendering in PNG (ad esempio Iz=Icm+MR^{{2}} diventa {\emph I}z=Icm+MR^{{2}}) .

Esempi

Polinomio di secondo grado

ax^{2}+bx+c=0

<math>ax^2 + bx + c = 0</math>

Polinomio di secondo grado (forzato in PNG)

ax^{2}+bx+c=0\,

<math>ax^2 + bx + c = 0\,</math>

Soluzioni di un'equazione di secondo grado

x_{{1,2}}={\frac  {-b\pm {\sqrt  {b^{2}-4ac}}}{2a}}

<math>x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}</math>

Parentesi e frazioni

2=\left({\frac  {\left(3-x\right)\times 2}{3-x}}\right)

<math>2 = \left( \frac{\left(3-x\right) \times 2}{3-x} \right)</math>

Integrali

\int _{a}^{x}\int _{a}^{s}f(y)\,dy\,ds=\int _{a}^{x}f(y)(x-y)\,dy

<math>\int_a^x \int_a^s f(y)\,dy\,ds = \int_a^x f(y)(x-y)\,dy</math>

Sommatorie

\sum _{{m=1}}^{\infty }\sum _{{n=1}}^{\infty }{\frac  {m^{2}\,n}{3^{m}\left(m\,3^{n}+n\,3^{m}\right)}}

<math>\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{m^2\,n}
{3^m\left(m\,3^n+n\,3^m\right)}</math>

Equazioni differenziali

u''+p(x)u'+q(x)u=f(x),\quad x>a

<math>u'' + p(x)u' + q(x)u=f(x),\quad x>a</math>

Numeri complessi

|{\bar  {z}}|=|z|,|({\bar  {z}})^{n}|=|z|^{n},\arg(z^{n})=n\arg(z)\,

<math>|\bar{z}| = |z|, |(\bar{z})^n| = |z|^n, \arg(z^n) = n \arg(z)\,</math>

Limiti

\lim _{{z\rightarrow z_{0}}}f(z)=f(z_{0})\,

<math>\lim_{z\rightarrow z_0} f(z)=f(z_0)\,</math>

Equazioni integrali

\phi _{n}(\kappa )={\frac  {1}{4\pi ^{2}\kappa ^{2}}}\int _{0}^{\infty }{\frac  {\sin(\kappa R)}{\kappa R}}{\frac  {\partial }{\partial R}}\left[R^{2}{\frac  {\partial D_{n}(R)}{\partial R}}\right]\,dR

<math>\phi_n(\kappa) = \frac{1}{4\pi^2\kappa^2} \int_0^\infty
\frac{\sin(\kappa R)}{\kappa R} \frac{\partial}{\partial R}\left[R^2\frac{\partial
D_n(R)}{\partial R}\right]\,dR</math>

Esempio generico

\phi _{n}(\kappa )=0.033C_{n}^{2}\kappa ^{{-11/3}},\quad {\frac  {1}{L_{0}}}\ll \kappa \ll {\frac  {1}{l_{0}}}\,

<math>\phi_n(\kappa) = 
0.033C_n^2\kappa^{-11/3},\quad \frac{1}{L_0}\ll\kappa\ll\frac{1}{l_0}\,</math>

Funzioni definite a pezzi

f(x)={\begin{cases}1&-1\leq x<0\\{\frac  {1}{2}}&x=0\\x&0<x\leq 1\end{cases}}

f(x) = \begin{cases}1 & -1 \le x < 0\\
\frac{1}{2} & x = 0\\x&0<x\le 1\end{cases}

Pedice prescritta

{}_{p}F_{q}(a_{1},...,a_{p};c_{1},...,c_{q};z)=\sum _{{n=0}}^{\infty }{\frac  {(a_{1})_{n}\cdot \cdot \cdot (a_{p})_{n}}{(c_{1})_{n}\cdot \cdot \cdot (c_{q})_{n}}}{\frac  {z^{n}}{n!}}\,

 <math>{}_pF_q(a_1,...,a_p;c_1,...,c_q;z) = \sum_{n=0}^\infty
\frac{(a_1)_n\cdot\cdot\cdot(a_p)_n}{(c_1)_n\cdot\cdot\cdot(c_q)_n}\frac{z^n}{n!}\,</math>

Voci correlate

Collegamenti esterni

Estratto da "https://wiki.dsy.it/index.php?title=Aiuto:Formule_matematiche_TeX&oldid=19145"