Aiuto:Prontuario TeX
In questa pagina presentiamo i segni e i costrutti facenti parte del sottolinguaggio TeX/LaTeX che consente l'inserimento di formule matematiche nelle pagine di Wikipedia. Le possibilità sono presentate in ordine alfabetico al fine di facilitare il ritrovamento da parte di chi possegga già qualche conoscenza di TeX, di LaTeX o delle formule per le pagine di Wikipedia.
In questa pagina si intendono anche fornire esempi tendenzialmente significativi, anche al fine di stimolare la omogeneità delle notazioni.
B
binomiali, coefficienti
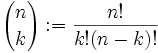 {n \choose k} := \frac{n!}{k!(n-k)!}
{n \choose k} := \frac{n!}{k!(n-k)!}
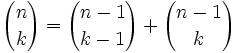 {n \choose k} = (n-1 \choose k-1} + (n-1 \choose k}
{n \choose k} = (n-1 \choose k-1} + (n-1 \choose k}
C
calligrafica / fonte : v. fonti speciali
complessi / espressioni per numeri
 z = x+iy = \rho e^{i\theta} = |z| e^{i \arg z}
z = x+iy = \rho e^{i\theta} = |z| e^{i \arg z} 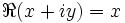 \Re(x+iy) = x
\Re(x+iy) = x 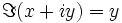 \Im(x+iy) = y
\Im(x+iy) = y
D
derivate
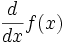 {d\over dx} f(x)
{d\over dx} f(x) 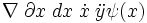 \nabla \; \partial x \; dx \; \dot x \; \ddot y \psi(x)
\nabla \; \partial x \; dx \; \dot x \; \ddot y \psi(x) 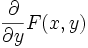 {\partial \over \partial y} F(x,y)
{\partial \over \partial y} F(x,y)
determinanti
![\det \left[{\frac {\partial }{\partial x_{i}}}{\frac {\partial }{\partial x_{j}}}\,|\,1\leq i,j\leq n\right]](/images/math/4/6/4/4649061b9b0ee5cf82d92f3b9a7f12ea.png)
- \det\left[ \frac{\partial}{\partial x_i}\frac{\partial}{\partial x_j} \,|\, 1\leq i,j\leq n \right]
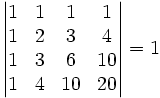
- \begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \\ 1 & 3 & 6 & 10 \\ 1 & 4 & 10 & 20 \end{vmatrix} = 1
disponibili / segni
 \heartsuit \heartsuit |
 \spadesuit \spadesuit |
 \clubsuit \clubsuit |
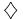 \diamondsuit \diamondsuit
|
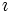 \imath \imath |
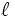 \ell \ell
|
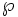 \wp \wp |
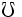 \mho \mho
|
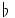 \flat \flat |
 \natural \natural |
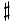 \sharp \sharp |
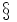 \mathcal{x} \mathcal{x}
|
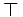 \top \top |
 \bot \bot |
 \Box \Box |
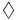 \Diamond \Diamond
|
E
ebraiche / lettere
\aleph 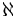 \beth
\beth 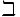 \gimel
\gimel 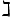 \daleth
\daleth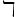
entità particolari
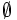 \empty \empty |
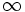 \infty \infty |
 \hbar \hbar
|
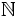 \N \N |
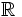 \R \R
|
esponenziali
10^{a+b} 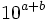 \,10^{a+b}\,
\,10^{a+b}\, 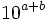 e^{-x^2}
e^{-x^2} 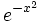
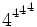 {{4^4}^4}^4
{{4^4}^4}^4 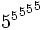 {{{5^5}^5}^5}^5
{{{5^5}^5}^5}^5
F
fonti / confronto
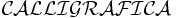 \mathcal{CALLIGRAFICA}
\mathcal{CALLIGRAFICA}
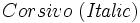 Corsivo\ \mathrm{(Italic)
Corsivo\ \mathrm{(Italic)
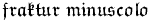 \mathfrak{fraktur\ minuscolo
\mathfrak{fraktur\ minuscolo
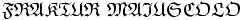 \mathfrak{FRAKTUR\ MAIUSCOLO}
\mathfrak{FRAKTUR\ MAIUSCOLO}
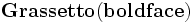 \mathbf{Grassetto (boldface)}
\mathbf{Grassetto (boldface)}
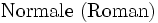 \mathrm{Normale\ (Roman)
\mathrm{Normale\ (Roman)
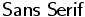 \mathbb{Sans\ Serif}
\mathbb{Sans\ Serif}
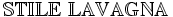 \mathbb{STILE\ LAVAGNA}
\mathbb{STILE\ LAVAGNA}
fraktur / fonte
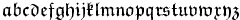 \mathfrak{abcdefghijklm} \mathfrak{nopqrstuvwxyz}
\mathfrak{abcdefghijklm} \mathfrak{nopqrstuvwxyz}
 \mathfrak{ABCDEFGHIJKLM} \mathfrak{NOPQRSTUVWXYZ}
\mathfrak{ABCDEFGHIJKLM} \mathfrak{NOPQRSTUVWXYZ}
frazioni
{a\over b} 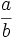 \frac{x+a}{x^2-2x+5}
\frac{x+a}{x^2-2x+5} 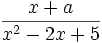
frecce
\leftarrow  |
\rightarrow  |
\uparrow 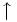
|
\longleftarrow  |
\longrightarrow  |
\downarrow 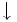
|
\Leftarrow 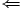 |
\Rightarrow 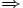 |
\Uparrow 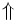
|
\Longleftarrow  |
\Longrightarrow  |
\Downarrow 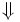
|
\leftrightarrow  |
\updownarrow 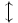
| |
\Leftrightarrow 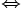 |
\Longleftrightarrow  |
\Updownarrow 
|
\to  |
\mapsto  |
\longmapsto 
|
\hookleftarrow 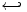 |
\hookrightarrow  |
\nearrow 
|
\searrow  |
\swarrow  |
\nwarrow 
|
funzioni standard / simboli per le
| \arccos | \cos | \csc | \exp | \ker | \limsup | \min | \sinh |
| \arcsin | \cosh | \deg | \gcd | \lg | \ln | \Pr | \sup |
| \arctan | \cot | \det | \hom | \lim | \log | \sec | \tan |
| \arg | \coth | \dim | \inf | \liminf | \max | \sin | \tanh |
G
geometria / simboli per la
 \triangle
\triangle 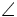 \angle
\angle
grassetto / caratteri in
| lettere normali | \mathbf{x}, \mathbf{y}, \mathbf{Z} | 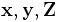
|
| lettere greche | \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma} | 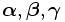
|
greche / lettere
\alpha , 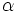 |
\vartheta , 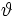 |
\varpi , 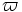 |
\chi , 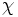 |
\Eta , 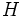 |
\Pi , 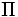
|
\beta , 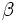 |
\iota , 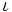 |
\rho , 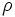 |
\psi , 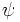 |
\Theta , 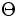 |
\Rho , 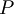
|
\gamma , 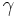 |
\kappa , 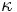 |
\varrho , 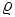 |
\omega , 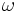 |
\Iota , 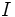 |
\Sigma , 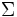
|
\delta , 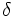 |
\lambda , 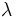 |
\sigma , 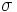 |
\Alpha , 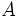 |
\Kappa , 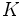 |
\Tau , 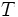
|
\epsilon , 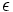 |
\mu , 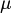 |
\varsigma ,  |
\Beta , 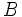 |
\Lambda , 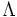 |
\Upsilon , 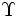
|
\varepsilon , 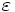 |
\nu , 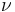 |
\tau , 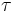 |
\Gamma , 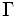 |
\Mu , 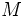 |
\Phi , 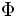
|
\zeta , 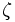 |
\xi , 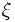 |
\upsilon , 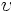 |
\Delta ,  |
\Nu , 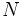 |
\Chi , 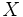
|
\eta , 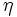 |
o (gewoon o) , 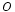 |
\phi , 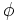 |
\Epsilon , 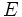 |
\Xi , 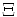 |
\Psi , 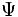
|
\theta , 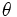 |
\pi ,  |
\varphi , 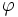 |
\Zeta , 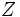 |
O (gewoon O), 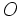 |
\Omega , 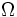
|
I
insiemi / espressioni concernenti
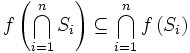 f\left(\bigcap_{i=1}^n S_i\right) \subseteq \bigcap_{i=1}^n f\left(S_i\right)
f\left(\bigcap_{i=1}^n S_i\right) \subseteq \bigcap_{i=1}^n f\left(S_i\right)
integrali
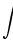 \int
\int 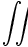 \iint
\iint 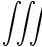 \iiint
\iiint 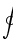 \oint
\oint
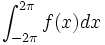 \int_{-2\pi}^{2\pi} f(x) dx
\int_{-2\pi}^{2\pi} f(x) dx
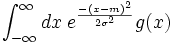 \int_{-\infty}^\infty dx\;e^{-(x-m)^2\over 2\sigma^2} g(x)
\int_{-\infty}^\infty dx\;e^{-(x-m)^2\over 2\sigma^2} g(x)
L
limiti
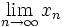 \lim_{n \to \infty}x_n
\lim_{n \to \infty}x_n
logica
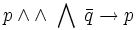 p \land \wedge \; \bigwedge \; \bar{q} \to p\
p \land \wedge \; \bigwedge \; \bar{q} \to p\
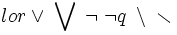 lor \vee \; \bigvee \; \lnot \; \neg q \; \setminus \; \smallsetminus
lor \vee \; \bigvee \; \lnot \; \neg q \; \setminus \; \smallsetminus
M
matrici
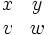 \begin{matrix} x & y \\ v & w \end{matrix}
\begin{matrix} x & y \\ v & w \end{matrix}
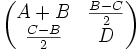 \begin{pmatrix} A+B & {B+C\over 2} \\ {B+c\over 2} & D \end{pmatrix}
\begin{pmatrix} A+B & {B+C\over 2} \\ {B+c\over 2} & D \end{pmatrix}
 \begin{vmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 \\ 1 & 3 & 6 & 10 & 15 \\ 1 & 4 & 10 & 20 & 35 \\ 1 & 5 & 15 & 35 & 70 \end{vmatrix}
\begin{vmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 & 5 \\ 1 & 3 & 6 & 10 & 15 \\ 1 & 4 & 10 & 20 & 35 \\ 1 & 5 & 15 & 35 & 70 \end{vmatrix}
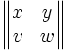 \begin{Vmatrix} x & y \\ v & w \end{Vmatrix}
\begin{Vmatrix} x & y \\ v & w \end{Vmatrix}
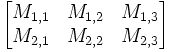 \begin{bmatrix} M_{1,1}&M_{1,2}&M_{1,3}\\M_{2,1}&M_{2,2}&M_{2,3} \end{bmatrix}
\begin{bmatrix} M_{1,1}&M_{1,2}&M_{1,3}\\M_{2,1}&M_{2,2}&M_{2,3} \end{bmatrix}
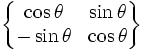 \begin{Bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{Bmatrix}
\begin{Bmatrix}\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{Bmatrix}
![{\begin{vmatrix}{\begin{bmatrix}x&y\\v&w\end{bmatrix}}&{\begin{bmatrix}a\\b\end{bmatrix}}\\{\begin{bmatrix}a&b\end{bmatrix}}&[1]\end{vmatrix}}](/images/math/b/4/2/b4244aa377146be875630fbb6df8da87.png) \begin{vmatrix} \begin{bmatrix} x & y \\ v & w \end{bmatrix} & \begin{bmatrix} a \\ b \end{bmatrix} \\ \begin{bmatrix} a & b \end{bmatrix} & [1] \end{vmatrix}
\begin{vmatrix} \begin{bmatrix} x & y \\ v & w \end{bmatrix} & \begin{bmatrix} a \\ b \end{bmatrix} \\ \begin{bmatrix} a & b \end{bmatrix} & [1] \end{vmatrix}
 \begin{bmatrix} x_{11}&x_{12}&\cdots&x_{1n} \\ x_{21}&x_{22}&\cdots&x_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ x_{m1}&x_{m2}&\cdots& x_{mn} \end{bmatrix}
\begin{bmatrix} x_{11}&x_{12}&\cdots&x_{1n} \\ x_{21}&x_{22}&\cdots&x_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ x_{m1}&x_{m2}&\cdots& x_{mn} \end{bmatrix}
moduli
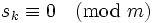 s_k \equiv 0 \pmod{m}
s_k \equiv 0 \pmod{m}
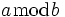 a \bmod b
a \bmod b
N
negazione di relazioni si ottiene premettendo la macro \not
\not\leq  ) \not\sim
) \not\sim 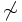 \not\models
\not\models 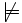 \not=
\not= 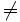 \not<
\not< 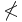 . . . .
. . . .
neretto / caratteri in v. grassetto / caratteri in
O
operatori binari
 \pm \pm |
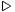 \triangleright \triangleright |
 \setminus \setminus |
 \circ \circ
|
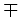 \mp \mp |
 \times \times |
 \bullet \bullet |
 \star \star
|
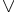 \vee \vee |
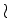 \wr \wr |
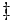 \ddagger \ddagger |
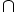 \cap \cap
|
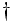 \dagger \dagger |
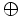 \oplus \oplus |
 \smallsetminus \smallsetminus |
 \cdot \cdot
|
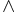 \wedge \wedge |
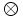 \otimes \otimes |
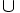 \cup \cup |
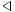 \triangleleft \triangleleft
|
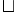 \mathcal{t} \mathcal{t} |
 \mathcal{u} \mathcal{u}
|
operatori n-ari (v.a. produttoria, sommatoria)
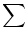 \sum \sum |
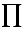 \prod \prod |
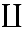 \coprod \coprod
|
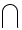 \bigcap \bigcap |
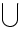 \bigcup \bigcup |
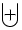 \biguplus \biguplus
|
 \bigodot \bigodot |
 \bigoplus \bigoplus |
 \bigotimes \bigotimes
|
 \bigsqcup \bigsqcup |
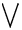 \bigvee \bigvee |
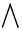 \bigwedge \bigwedge
|
operatori unari
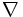 \nabla
\nabla 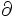 \partial
\partial 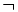 \neg
\neg
 \sim
\sim
P
parentesi
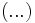 (...) (...) |
![[...]](/images/math/3/6/d/36d597b1796275fe48088204309e3ea6.png) [...] [...] |
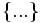 \{...\} \{...\}
| |
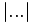 |...| |...| |
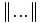 \|...\| \|...\|
|
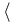 \langle \langle |
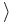 \rangle \rangle
|
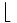 \lfloor \lfloor |
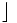 \rfloor \rfloor
|
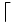 \lceil \lceil |
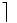 \rceil \rceil
|
parentesi adattabili
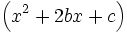 \left(x^2+2bx+c\right)
\left(x^2+2bx+c\right)
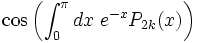 \cos\left(\int_0^\pi dx\;e^{-x} P_{2k}(x)\right)
\cos\left(\int_0^\pi dx\;e^{-x} P_{2k}(x)\right)
produttoria
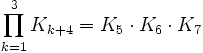 \prod_{k=1}^3 K_{k+4} = K_5\cdot K_6\cdot K_7
\prod_{k=1}^3 K_{k+4} = K_5\cdot K_6\cdot K_7
puntini \ldots  \cdots
\cdots  \vdots
\vdots  \ddots
\ddots  (v.a. matrici)
(v.a. matrici)
Q
quantificatori 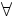 \forall
\forall 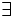 \exists
\exists
 \forall_{i \in \N, j \in \N \setminus \{0\}} (i/j \in \mathbb{Q})
\forall_{i \in \N, j \in \N \setminus \{0\}} (i/j \in \mathbb{Q})
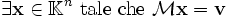
- \mathbf{x} \in \mathbb{K}^n \ \mbox{tale che}\ \mathcal{M} \mathbf{x} = \mathbf{v}
R
radici
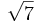 \sqrt 7
\sqrt 7 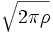 \sqrt{2\pi\rho}
\sqrt{2\pi\rho}
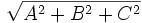 \sqrt{A^2+B^2+C^2}
\sqrt{A^2+B^2+C^2}
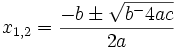 x_{1,2} = \frac{-b\pm\sqrt{b^-4ac}}{2a}
x_{1,2} = \frac{-b\pm\sqrt{b^-4ac}}{2a}
![{\sqrt[ {3}]3}](/images/math/a/3/c/a3cf81dd55c6885823104e19031ea709.png) \sqrt[3]3
\sqrt[3]3 ![{\sqrt[ {h+k}]{a\pm \sin(2k\pi )}}](/images/math/f/b/e/fbe83812ccddcb738d5c6ca59314a0da.png) \sqrt[h+k]{ a\pm\sin(2k\pi)} }
\sqrt[h+k]{ a\pm\sin(2k\pi)} }
raggruppamenti di simboli
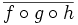 \overline{f\circ g\circ h} \overline{f\circ g\circ h} |
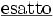 \underline{\mbox{esatto}} \underline{\mbox{esatto}}
|
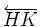 \overleftarrow{HK} \overleftarrow{HK} |
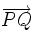 \overrightarrow{PQ} \overrightarrow{PQ}
|
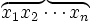 \overbrace{x_1x_2\cdots x_n} \overbrace{x_1x_2\cdots x_n} |
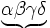 \underbrace{\alpha\beta\gamma\delta} \underbrace{\alpha\beta\gamma\delta}
|
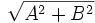 \sqrt{A^2+B^2} \sqrt{A^2+B^2} |
![{\sqrt[ {3}]{p^{3}-{qr \over 3}}}](/images/math/c/4/7/c47a9cefcac11a0cac6a692c76ac5315.png) \sqrt[n]{p^3-{qr\over3}} \sqrt[n]{p^3-{qr\over3}}
|
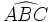 \widehat{ABC} \widehat{ABC}
|
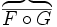 \overbrace{\overline{F\circ G}}
\overbrace{\overline{F\circ G}}
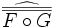 \widehat{\overline{\overline{F\circ G}}}
\widehat{\overline{\overline{F\circ G}}}
relazioni
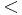 \,<\, \,<\, |
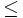 \leq \leq |
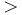 \,>\, \,>\, |
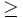 \geq \geq
|
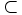 \subset \subset |
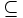 \subseteq \subseteq |
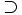 \supset \supset |
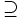 \supseteq \supseteq
|
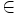 \in \in |
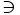 \ni \ni |
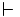 \vdash \vdash |
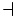 \mathcal{a} \mathcal{a}
|
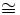 \cong \cong |
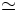 \simeq \simeq |
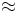 \approx \approx |
 \sim \sim
|
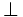 \perp \perp |
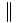 \| \| |
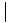 \mid \mid |
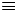 \equiv \equiv
|
 \frown \frown |
 \smile \smile |
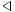 \triangleleft \triangleleft |
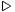 \triangleright \triangleright
|
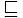 \mathcal{v} \mathcal{v} |
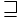 \mathcal{w} \mathcal{w} |
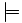 \models \models
|
S
sans serif / fonte
 \mathsf{abcdefghijklm} \mathsf{nopqrstuvwxyz}
\mathsf{abcdefghijklm} \mathsf{nopqrstuvwxyz}
 \mathsf{ABCDEFGHIJKLM} \mathsf{NOPQRSTUVWXYZ}
\mathsf{ABCDEFGHIJKLM} \mathsf{NOPQRSTUVWXYZ}
sistemi di equazioni
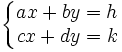 \left{\begin{matrix}ax+by=h \\ cx+dy=k\end{matrix}\right.
\left{\begin{matrix}ax+by=h \\ cx+dy=k\end{matrix}\right.
sommatoria
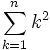 \sum_{k=1}^n k^2
\sum_{k=1}^n k^2
T
tensori e simili
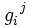 g_i^{\ j}
g_i^{\ j}
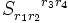 S_{r_1r_2}^{\ \ \ \ r_3r_4}
S_{r_1r_2}^{\ \ \ \ r_3r_4} 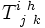 T_{\ j\ k}^{i\ h}
T_{\ j\ k}^{i\ h}
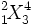 {}_1^2\!X_3^4
{}_1^2\!X_3^4
V
vettori
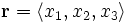 \mathbf{r}=\langle x_1,x_2,x_3\rangle
\mathbf{r}=\langle x_1,x_2,x_3\rangle
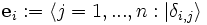 \mathbf{e}_i :\!= \langle j=1,...,n :| \delta_{i,j} \rangle
\mathbf{e}_i :\!= \langle j=1,...,n :| \delta_{i,j} \rangle
VARIE
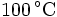 100\,^{\circ}\mathrm{C}
100\,^{\circ}\mathrm{C}
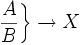 \left. {A \over B} \right\} \to X
\left. {A \over B} \right\} \to X