Calcolo probabilità e statistica matematica
| Questa è una pagina di introduzione al corso: contiene i turni, le modalità d'insegnamento, alcune informazioni generali ed eventuali giudizi sul corso in questione. Se sei giunto qui passando da un link, puoi tornare indietro e correggerlo in modo che punti direttamente alla voce appropriata. |
Indice
- 1 Turni
- 2 A.A. passati
- 3 Informazioni
- 4 Diario del corso 2007/2008
- 4.1 Lezione del 01/10/07 - Teoria
- 4.2 Lezione del 05/10/07 - Teoria
- 4.3 Lezione del 08/10/07 - Teoria
- 4.4 Lezione del 12/10/07 - Teoria
- 4.5 Lezione del 19/10/07 - Teoria
- 4.6 Lezione del 22/10/07 - Teoria
- 4.7 Lezione del 24/10/07 - Esercitazione "Corso Ombra"
- 4.8 Lezione del 26/10/07 - Teoria
- 4.9 Lezione del 29/10/07 - Teoria
- 4.10 Lezione del 31/10/07 - Esercitazione "Corso Ombra"
- 4.11 Lezione del 02/11/07 - PONTE
- 4.12 Lezione del 05/11/07 - Teoria
- 4.13 Lezione del 07/11/07 - Esercitazione "Corso Ombra"
- 4.14 Lezione del 09/11/07 - Teoria
- 4.15 Lezione del 12/11/07 - Teoria
- 4.16 Lezione del 14/11/07 - Esercitazione "Corso Ombra"
- 4.17 Lezione del 16/11/07 - Teoria
- 4.18 Lezione del 19/11/07 - Teoria
- 4.19 Lezione del 21/11/07 - Esercitazione "Corso Ombra"
- 4.20 Lezione del 23/11/07 - Teoria
- 4.21 Lezione del 26/11/07 - Teoria
- 4.22 Lezione del 28/11/07 - Esercitazione "Corso Ombra"
- 4.23 Lezione del 30/11/07 - Teoria
- 4.24 Lezione del 03/12/07 - Teoria
- 4.25 Lezione del 05/12/07 - Esercitazione "Corso Ombra"
- 4.26 Lezione del 07/12/07 - FESTA
- 4.27 Lezione del 10/12/07 - Teoria
- 4.28 Lezione del 12/12/07 - Esercitazione "Corso Ombra"
- 4.29 Lezione del 14/12/07 - Teoria
- 4.30 Lezione del 17/12/07 - Teoria
- 4.31 Lezione del 19/12/07 - Esercitazione "Corso Ombra"
- 4.32 Lezione del 21/12/07 - Teoria
- 4.33 Lezione del 07/01/08 - Teoria
- 4.34 Lezione del 11/01/08 - Teoria
- 4.35 Lezione del 14/01/08 - Teoria
Turni
A.A. passati
- (De Falco) T1, A.A. 2007-2008
- (De Falco) T1, A.A. 2006-2007
- (Apolloni) T2, A.A. 2006-2007
- (De Falco) T1, A.A. 2005-2006
Informazioni
Corso del primo semestre, il superamento di quest'esame da diritto a 6 CFU.
- Docente: Bruno Apolloni
- Url del corso
Obiettivi del corso
Fornire gli elementi di base per la costruzione di modelli probabilistici e per l’analisi statistica di fenomeni aleatori.
Modalità d'esame
- Scritto
- Orale
Propedeuticità consigliate e prerequisiti
- Istituzioni matematiche
- Rudimenti di insiemistica e di calcolo differenziale ed integrale.
Programma del corso
- Legame tra conoscenza e aleatorietà
- Proprietà corrette su insiemi di dati incerti
- Misure di probabilità
- Elementi di calcolo combinatorio
- Variabili aleatorie
- Da uno a più bit per definire una variabile
- Aggregati di variabili aleatorie
- Funzioni di variabili aleatorie
- Teoremi limiti
- Inferenza statistica
- L’approccio predittivo
- Intervalli di confidenza
- Stimatori puntuali
- Test di ipotesi
Metodi didattici
Il corso si articola attraverso lezioni teoriche volte spiegare i ragionamenti alla base della modellistica probabilistica e dell’inferenza statistica ed esercitazioni nelle quali a questi ragionamenti si da un riscontro operativo, in termini di regole ed algoritmi per definire quantitativamente decisioni in ambito incerto.
Giudizio sul corso
I giudizi di seguito espressi sono il parere personale degli studenti, e potrebbero non rispecchiare il parere medio dei frequentanti. Non vi è comunque alcun intento di mettere alla gogna i docenti del corso!
Diario del corso 2007/2008
Lezione del 01/10/07 - Teoria
- Definizioni di ESITO, EVENTO, PROBABILITA' (prima meta' del cap.1 del MOOD)
Lezione del 05/10/07 - Teoria
- Assiomi di Kolmogorov
- Evento certo
- Evento impossibile
Lezione del 08/10/07 - Teoria
- Probabilita' dell'unione come somma delle probabilita'
Lezione del 12/10/07 - Teoria
- Probabilita' condizionata (Teorema di Bayes o Chain Rule)
- Teorema delle probabilita' totali
Lezione del 19/10/07 - Teoria
- Funzione indicatrice (o caratteristica)
- Variabili casuali
- Funzione di ripartizione
- Distribuzione Bernoulliana Uniforme
Lezione del 22/10/07 - Teoria
- Funzione di ripartizione
- Probabilita' condizionata
- Binomiale: Sm e P(Sm=k)
Lezione del 24/10/07 - Esercitazione "Corso Ombra"
Tema d'esame del 13/09/2007: Svolgimento
Lezione del 26/10/07 - Teoria
- Variabile Casuale Binomiale
- Funzione di densita' (o funzione di probabilita' discreta) di Var.Cas. Binomiale
Lezione del 29/10/07 - Teoria
- Distribuzione Binomiale
- Legge Debole dei Grandi Numeri
- Chebyshev
- Moda
Lezione del 31/10/07 - Esercitazione "Corso Ombra"
Tema d'esame del 13/09/2007: Parole chiave
- dimostrazione "4 dummies" di Chebyshev
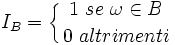
quindi 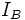 e' BERNOULLIANA.
e' BERNOULLIANA.
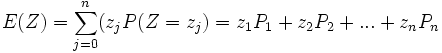
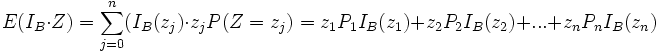
=> se tutti i termini sono tali che 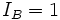 , allora
, allora 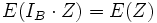
=> ma se almeno un termine e' tale che 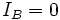 , allora
, allora 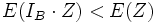
=> in nessun caso posso avere 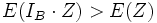
premesso questo, ne segue che:
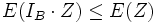
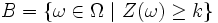
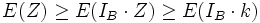
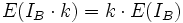
ma 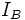 e' bernoulliana, allora:
e' bernoulliana, allora:
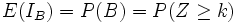
quindi:
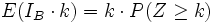
riassumendo:
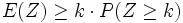
percio' dividendo per k e invertendo i termini e il verso della disequazione:
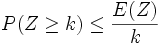
Lezione del 02/11/07 - PONTE
PONTE
Lezione del 05/11/07 - Teoria
- Valore atteso
- Varianza
- Chebyshev
Lezione del 07/11/07 - Esercitazione "Corso Ombra"
Tema d'esame del 05/07/2007: Svolgimento
Lezione del 09/11/07 - Teoria
- Esempio tema d'esame del 13/09/2007
Lezione del 12/11/07 - Teoria
- Chebyshev sul continuo
- Covarianza
- Varianza della Binomiale (var(Sm))
Lezione del 14/11/07 - Esercitazione "Corso Ombra"
- Tema d'esame del 05/07/2007: Svolgimento
- Tema d'esame del 05/07/2007: Parole chiave:
- V.C. continua
- V.C. uniforme
- V.C. esponenziale
- V.C. poissoniana
- approssimazione della binomiale con la poissoniana
Lezione del 16/11/07 - Teoria
Riscrittura di Chebyshev dopo note su:
- E(X)
- Proprieta' di E(X)
- Proprieta' della var(X)
- cov(X,Y)
Legge Debole dei Grandi Numeri
Lezione del 19/11/07 - Teoria
Chebyshev
Lezione del 21/11/07 - Esercitazione "Corso Ombra"
Tema d'esame del 13/06/2007: Svolgimento
Lezione del 23/11/07 - Teoria
Svolto tema d'esame del 12/01/2005
Lezione del 26/11/07 - Teoria
- Svolto tema d'esame del 24/02/2000
- Polya - contagio
- Note sulla covarianza
Lezione del 28/11/07 - Esercitazione "Corso Ombra"
Tema d'esame del 13/06/2007: Parole chiave:
- Funzione di ripartizione
- Funzione di ripartizione congiunta
- Proprieta' Fx singola e multipla
- Funzione di densita' congiunta
- Distribuzioni condizionali
- Somma di variabili casuali
Lezione del 30/11/07 - Teoria
- Polya
- Chebyshev per la Binomiale
- Chebyshev per la Ipergeometrica
- var(Sm) con contagio
- Stima migliore sul problema delle viti (tema d'esame del 12/01/2005)
Lezione del 03/12/07 - Teoria
- Polya
- Distorsione stimatori
- Distribuzione Geometrica
- Probabilita' condizionata
Lezione del 05/12/07 - Esercitazione "Corso Ombra"
Tema d'esame del 12/01/2005: Svolgimento
Lezione del 07/12/07 - FESTA
FESTA
Lezione del 10/12/07 - Teoria
- Ipergeometrica
- Estrazioni indipendenti
- Estrazioni senza contagio
- Geometrica
Lezione del 12/12/07 - Esercitazione "Corso Ombra"
Lezione del 14/12/07 - Teoria
- Tema d'esame del 14/09/2005
- Tema d'esame del 14/01/2004
- Geometrica
- Chebyshev per la Geometrica
- Funzione generatrice dei momenti per la Geometrica:
Lezione del 17/12/07 - Teoria
- Normale
- Poissoniana
- Funzione generatrice dei momenti
Lezione del 19/12/07 - Esercitazione "Corso Ombra"
Lezione del 21/12/07 - Teoria
- Poissoniana
- Moda
- Somma di Poissoniane
- Gaussiana
- Normale
- Continua Uniforme
Lezione del 07/01/08 - Teoria
- Geometrica
- Esponenziale
- Relazione tra Geometrica ed Esponenziale
Lezione del 11/01/08 - Teoria
Ancora da fare
Lezione del 14/01/08 - Teoria
- Variabili Casuali Continue
- Distribuzione Normale

